Историја математике

Доказ из |Еуклидових елемената (око 300. п. н. е.), који се нашироко сматра најутицајнијим уџбеником свих времена.

Табела бројева

Подручје студија познато као историја математике првенствено је истраживање порекла открића у математици и, у мањој мери, истраживање математичких метода и нотација прошлости. Пре модерног доба и ширења знања широм света, писани примери нових математичких достигнућа изашли су на видело само на неколико локација. Од 3000. године п. н. е, месопотамијске државе Сумер, Акад и Асирија, праћене древним Египтом и левантинском државом Ебла, почеле су да користе аритметику, алгебру и геометрију у сврхе опорезивања, привреде, трговине, као и у проницању патерна у природи, на подручју астрономије и да бележе време и формулишу календаре.

Тешко је са сигурношћу тврдити када је и шта је почетак математике. Највероватније је да је то бројање. Оно што са сигурношћу можемо тврдити, на основу археолошких ископавања, је да у Египту и Месопотамији имамо прве писане податке нечега што можемо подвести под математичке списе. У Египту (види староегипатска математика) су то листови папируса (Рајндов папирус) а у Месопотамији глинене плочице.

Египћани и Стари Сумери су математику развијали за практичне потребе, највише за премеравање земље после изливања Нила, градњу канала, положај звезда, грађевинарство, итд. Треба напоменути да су Египћани знали за Питагорину теорему, али не у њеном облику c² = a² + b² већ као одређене једнакости. Примера ради ако су имали правоугли троугао са катетама 3 и 4 знали су да је хипотенуза 5, овај троугао се и данас назива египатски троугао.

Потом развој математике преузимају Стари Грци, који математици дају нову димензију односно почиње развој апстрактне математике, тј. математике која нема директну практичну примену. Они су први засновали аксиоматски приступ математици. Грци се највише баве геометријом, али и алгебром. За Грке је математика основа свега, па је тако на улазу у Академију стајао натпис: „Нека не улази онај који не зна геометрију“. Еуклидови „Елементи“ је књига која је представљала најбољи уџбеник из области геометрије све до краја 19. века и Хилберта. Геометрија је после Хеленистичког периода таворила све до Лобачевског.

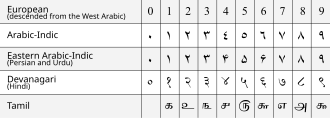
Исто тако постојала је математика и у Кини и Индији. Бројеви којима данас пишемо су дошли до Европе из Индије захваљујући Арапима. У средњем веку долази до престанка бављења математиком у хришћанском свету, па тако Јустинијан I забрањује рад Академији. Истовремено долази до процвата арапске математике. Почетком ренесансе и математика оживљава у Европи.

Литература

• Berggren, Lennart; Borwein, Jonathan M.; Borwein, Peter B. (2004), Pi: A Source Book, New York: Springer, ISBN 978-0-387-20571-7 
• Boyer, C.B. (1991) [1989], A History of Mathematics (2nd изд.), New York: Wiley, ISBN 978-0-471-54397-8 
• Cuomo, Serafina (2001), Ancient Mathematics, London: Routledge, ISBN 978-0-415-16495-5 
• Goodman, Michael, K.J. (2016), An introduction of the Early Development of Mathematics, Hoboken: Wiley, ISBN 978-1-119-10497-1 
• Gullberg, Jan (1997), Mathematics: From the Birth of Numbers, New York: W.W. Norton and Company, ISBN 978-0-393-04002-9 
• Joyce, Hetty (јул 1979), „Form, Function and Technique in the Pavements of Delos and Pompeii”, American Journal of Archaeology, 83 (3): 253—63, JSTOR 505056, doi:10.2307/505056. CS1 одржавање: Формат датума (веза)
• Katz, Victor J. (1998), A History of Mathematics: An Introduction (2nd изд.), Addison-Wesley, ISBN 978-0-321-01618-8 
• Katz, Victor J. (2007), The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11485-9 
• Needham, Joseph; Wang, Ling (1995) [1959], Science and Civilization in China: Mathematics and the Sciences of the Heavens and the Earth, 3, Cambridge: Cambridge University Press, ISBN 978-0-521-05801-8 
• Needham, Joseph; Wang, Ling (2000) [1965], Science and Civilization in China: Physics and Physical Technology: Mechanical Engineering, 4 (reprint изд.), Cambridge: Cambridge University Press, ISBN 978-0-521-05803-2 
• Sleeswyk, Andre (октобар 1981), „Vitruvius' odometer”, Scientific American, 252 (4): 188—200, Bibcode:1981SciAm.245d.188S, doi:10.1038/scientificamerican1081-188. CS1 одржавање: Формат датума (веза)
• Straffin, Philip D. (1998), „Liu Hui and the First Golden Age of Chinese Mathematics”, Mathematics Magazine, 71 (3): 163—81, doi:10.1080/0025570X.1998.11996627 
• Tang, Birgit (2005), Delos, Carthage, Ampurias: the Housing of Three Mediterranean Trading Centres, Rome: L'Erma di Bretschneider (Accademia di Danimarca), ISBN 978-88-8265-305-7. 
• Volkov, Alexei (2009), „Mathematics and Mathematics Education in Traditional Vietnam”, Ур.: Robson, Eleanor; Stedall, Jacqueline, The Oxford Handbook of the History of Mathematics, Oxford: Oxford University Press, стр. 153—76, ISBN 978-0-19-921312-2 
• Aaboe, Asger (1964). Episodes from the Early History of Mathematics. New York: Random House. 
• Bell, E.T. (1937). Men of Mathematics. Simon and Schuster. 
• Burton, David M. The History of Mathematics: An Introduction. McGraw Hill: 1997.
• Grattan-Guinness, Ivor (2003). Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences. The Johns Hopkins University Press. ISBN 978-0-8018-7397-3. 
• Kline, Morris. Mathematical Thought from Ancient to Modern Times.
• Struik, D.J. (1987). A Concise History of Mathematics, fourth revised edition. Dover Publications, New York.
• Gillings, Richard J. (1972). Mathematics in the Time of the Pharaohs. Cambridge, MA: MIT Press. 
• Heath, Sir Thomas (1981). A History of Greek Mathematics. Dover. ISBN 978-0-486-24073-2. 
• van der Waerden, B.L., Geometry and Algebra in Ancient Civilizations, Springer, (1983) ISBN 0-387-12159-5.
• Corry, Leo (2015), A Brief History of Numbers, Oxford University Press, ISBN 978-0198702597 
• Hoffman, Paul (1998). The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. Hyperion. ISBN 0-7868-6362-5. 
• Menninger, Karl W. (1969). Number Words and Number Symbols: A Cultural History of Numbers. MIT Press. ISBN 978-0-262-13040-0. 
• Stigler, Stephen M. (1990). The History of Statistics: The Measurement of Uncertainty before 1900. Belknap Press. ISBN 978-0-674-40341-3. 
• Berriman, A. E. (1956). The Babylonian quadratic equation. 
• Høyrup, Jens. „Pythagorean ‘Rule’ and ‘Theorem’ – Mirror of the Relation Between Babylonian and Greek Mathematics”. Ур.: Renger, Johannes. Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin (PDF). Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. стр. 393—407. 
• Joseph, G. G. (2000). The Crest of the Peacock. Princeton University Press. ISBN 0-691-00659-8. 
• Joyce, David E. (1995). „Plimpton 322”. 
• O'Connor, J. J.; Robertson, E. F. (децембар 2000). „An overview of Babylonian mathematics”. MacTutor History of Mathematics. CS1 одржавање: Формат датума (веза)
• Robson, Eleanor (2001). „Neither Sherlock Holmes nor Babylon: a reassessment of Plimpton 322”. Historia Math. 28 (3): 167—206. MR 1849797. doi:10.1006/hmat.2001.2317. 
• Robson, E. (2002). „Words and pictures: New light on Plimpton 322”. American Mathematical Monthly. Washington. 109 (2): 105—120. JSTOR 2695324. S2CID 33907668. doi:10.1080/00029890.2002.11919845. 
• Robson, E. (2008). Mathematics in Ancient Iraq: A Social History. Princeton University Press. 
• Toomer, G. J. (1981). Hipparchus and Babylonian Astronomy. 

Спољашње везе

• Рана математика (РТС, 16. април 2016)
• BBC (2008). The Story of Maths.
• Renaissance Mathematics, BBC Radio 4 discussion with Robert Kaplan, Jim Bennett & Jackie Stedall (In Our Time, Jun 2, 2005)

Образовни материјал

• MacTutor History of Mathematics archive (John J. O'Connor and Edmund F. Robertson; University of St Andrews, Scotland). An award-winning website containing detailed biographies on many historical and contemporary mathematicians, as well as information on notable curves and various topics in the history of mathematics.
• History of Mathematics Home Page (David E. Joyce; Clark University). Articles on various topics in the history of mathematics with an extensive bibliography.
• The History of Mathematics (David R. Wilkins; Trinity College, Dublin). Collections of material on the mathematics between the 17th and 19th century.
• Earliest Known Uses of Some of the Words of Mathematics (Jeff Miller). Contains information on the earliest known uses of terms used in mathematics.
• Earliest Uses of Various Mathematical Symbols (Jeff Miller). Contains information on the history of mathematical notations.
• Mathematical Words: Origins and Sources (John Aldrich, University of Southampton) Discusses the origins of the modern mathematical word stock.
• Biographies of Women Mathematicians (Larry Riddle; Agnes Scott College).
• Mathematicians of the African Diaspora (Scott W. Williams; University at Buffalo).
• Notes for MAA minicourse: teaching a course in the history of mathematics. (2009) (V. Frederick Rickey & Victor J. Katz).

Библиографије

• A Bibliography of Collected Works and Correspondence of Mathematicians archive dated 2007/3/17 (Steven W. Rockey; Cornell University Library).

Организације

• International Commission for the History of Mathematics

Часописи

• Historia Mathematica
• Convergence Архивирано на сајту Wayback Machine (8. септембар 2020), the Mathematical Association of America's online Math History Magazine
• History of Mathematics Архивирано на сајту Wayback Machine (4. октобар 2006) Math Archives (University of Tennessee, Knoxville)
• History/Biography The Math Forum (Drexel University)
• History of Mathematics (Courtright Memorial Library).
• History of Mathematics Web Sites Архивирано на сајту Wayback Machine (25. мај 2009) (David Calvis; Baldwin-Wallace College)
• History of mathematics на сајту Curlie (језик: енглески)
• Historia de las Matemáticas (Universidad de La La guna)
• História da Matemática (Universidade de Coimbra)
• Using History in Math Class
• Mathematical Resources: History of Mathematics (Bruno Kevius)
• History of Mathematics (Roberta Tucci)