Случајна шетња
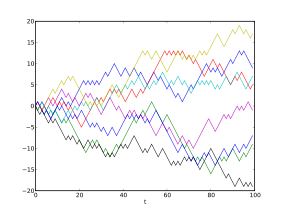
Случајна шетња (случајни ход) је математичка формализација пута који се састоји од низа случајних корака. На пример, путања праћења молекула као што путује у течност или гас, за претрагу пута сакупљањем животиње, цена једне променљиве акције и финансијски статус коцкара могу се моделирати као случајне шетње, иако то не може бити истински случајно у стварности. Термин случајног хода је први пут уведео Карл Пеарсон 1905.[1] Случајне шетње су коришћене у многим областима: екологија, економија, психологија, информатика, физика, хемија, и биологија.[2][3][4][5][6][7][8][9] Случајне шетње објашњавају уочена понашања многих процеса у овим областима, и на тај начин служе као темељни модел за снимљене стокестик активности.
Различити типови случајних шетњи су од интереса. Често се претпоставља да су Марковљеви ланци или Марковљеви процеси, али и друге, много компликованије шетње су такође од интереса. Неке слободне шетње су на графиконима, друге на линијама, у авиону, у вишим димензијама, или чак заобљеним површинама, док су неке случајне шетње у групама. Слободне шетње такође варирају у односу на временски параметар. Често је шетња у дискретном времену, а потиче из природних бројева, као у к_0, к_1, X_2, \ дотс. Међутим, неке шетње праве своје кораке у случајним размацима, а у том случају положај X_т је дефинисана за бесконачно време т \ ге 0. Одређени случајеви или границе случајних шетњи укључују Леви лет. Случајне шетње су везане за моделе дифузије и представљају основну тему дискусија Марковог рада. Неколико својстава случајних шетњи, укључујући и распростирање дистрибуције, први пролаза времена и сусрет стопа, су интензивно проучавани.
Решетке случајне шетње[уреди | уреди извор]
Популарни модел случајне шетње је случајна шетња на регуларној решетки, где на сваком кораку локација скаче на друго место, према неким вероватноћама расподеле. У принципу случајне шетње, локација може да скочи само са суседних места решетке, формирајући пут решетке. У једноставној симетричној случајној шетњи на локалном нивоу коначне решетке, вероватноћа за локацију скоковима на сваки његови најближи сусед је иста. Најбољи пример је проучавање случајне шетње на д-димензионални целим решеткама (понекад се назива хиперцубиц решетке) \ матхбб З ^ ум.
Једно димензијална слободна шетња[уреди | уреди извор]
Основни пример случајне шетње је случајна шетња на цео број линије, \ матхбб З, који почиње у 0 и на сваком кораку креће +1 или -1 са истом вероватноћом.
Ова шетња може се илустровати на следећи начин. Маркер је постављен на нулу на број линије и кованица је преврнута. Ако падне на главу, маркер се помера једну јединицу са десне стране. Ако падне на репове, маркер се помера једну јединицу са леве стране. Након пет бацања, маркер може сада бити на 1, -1, 3, -3, 5 или -5. Са пет бацања, три главе и два репа, у било ком редоследу ће слетети на 1. Постоји 10 начина за слетање на 1 (окретањем три главе и два репа), 10 начина слетања на -1 (окретањем три репа и две главе), 5 начини слетања на 3 (окретањем четири главе и један реп), 5 начине слетања на -3 (окретањем четири репа и једна глава), 1 пут слетању на 5 (окретањем пет глава), и 1 начин слетању на -5 (окретањем пет репа). Погледајте слику испод за илустрацију могућих исхода од 5 окрета.




Да бисмо формално дефинисали ову шетњу, узимамо независне случајне променљиве , где је свака променљива 1 или -1, са вероватноћом за обе вредности 50% и поставимо и Серија се зове једноставно случајна шетња . Ова серија (збир секвенци од −1s до 1s) даје удаљеност шетње, ако је сваки део шетње дужина једног. Очекивано од је нула. То јест, средња вредност свих бачених новчића приближава се нули како се број бацања повећава. Ово следи од коначних додатака имовине очекивања:
Слична рачуница, користећи независност случајних променљивих и чињеница да , показује да:
То наговештава да , очекивани превод растојања након н корака, треба да буде реда. На пример,[10]
Овај резултат показује да је дифузија неефикасна за мешање због начина на који се квадратни корен понаша за велико .
Колико пута ће случајна шетња да пређе граничну линију уколико је дозвољено да настави шетњу заувек? Једноставна случајна шетња по \ матхбб З ће прећи сваку тачку неограничен број пута. Овај резултат има много имена: Ниво прелаз феномен, понављање или пропаст коцкар је. Разлог за презиме гласи: коцкар са ограниченом количином новца ће на крају изгубити када играју фер утакмицу против једне банке са бесконачним количином новца. Новац коцкара ће обављати случајну шетњу, а то ће достићи нулу у неком тренутку, и игра ће бити готова.
Ако су а и б позитивни цели бројеви, тада је очекивани број корака до једнодимензионалног принципа случајне шетње са почетком у првим ударцима б или -а је АБ. Вероватноћа је да ће ова шетња погодити Б пре него што -а је А / (А + Б), што се може извести из чињенице да једноставна случајна шетња представља лажне узде.
Неки од наведених резултати може бити изведен из својстава Паскаловог троугла. Број различитих слојева н кораке где сваки корак је +1 или -1 је 2н. Из просте случајне шетње, свака од ових шетњи је подједнако вероватна. Да би Сн био једнак са бројем к потребно је и довољно да број +1 у шетњи премашује оне -1 до к. Број шетњи које задовољавају је једнак броју начина избора (н - к) / 2 са н које је број дозвољених потеза, означен. Да ово има значење, потребно је да су н и к парни бројеви. Дакле, вероватноћа да је једнако . Што представља уносе Паскаловог троугла у смислу факторијала и коришћења Стирлинг формуле, могу се постићи добре процене за ове вероватноће за велике вредности н.
Ако је простор ограничен на \ матхбб З + за краткотрајно, број начина на који ће случајна шетња да слете на сваки број има пет бацања и може да се прикаже као {0,5,0,4,0,1}.
Овај однос са Паскаловим троуглом је доказан за мале вредности н. Ако креће од нуле, једина могућност ће бити да остане на нули. Међутим, у једном опет, постоји једна шанса од слетања на -1 или једно могуће спуштање на 1. У два наврата, маркер на 1 да пређе на 2 или назад на нулу. Маркер на -1, да пређе на -2 или назад на нулу. Дакле, постоји једна шанса од слетања на -2, две шансе за слетање на нулу, а једно могуће слетање на 2.
| k | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
Теорема централне границе и закон понављања логаритма описују важне аспекте понашања принципа случајне шетње \mathbb Z. Конкретно, претходно се подразумева да н расте, приступ вероватноће (пропорционална броју у сваком реду) са нормалном расподелом.
[11]Као директна генерализација, могу се узети у обзир случајне шетње на кристалној летвици (Инфините износа Абелеви покрива графиконе преко коначних графова). Заправо је могуће успоставити централну граничну теорему и теорему великих девијација у овом окружењу.
Као Марков ланац[уреди | уреди извор]
Једнодимензионална случајна шетња може се посматрати као Марков ланац чије стање простора је дато по облику целих За неке бројеве п задовољава се, вероватноћа прелаза (вероватноћа Пи ј преласка из стања да се наведе ј) и дају:
Више димензије[уреди | уреди извор]

Замислите сада пијаница који случајно шета у идеализованом граду. Град је ефективно бесконачан и распоређен у квадратну мрежу, и на сваком пресеку пијанац бира једну од четири могућа пута (укључујући и онај из којег је дошао), са једнаком вероватноћом. Формално, ово је случајна шетња одређена свим тачакама у равни са целим координатама.
Да ли ће се пијанац икада вратити својој кући из бара? То је 2-димензионални еквивалент проблема нивоа прелаза који је раније описан. Испоставило се да је скоро сигурно да ће у 2-димензионалној случајној шетњи, али и са 3 димензије или више, вероватноћа повратка у просеку смањује како се број димензија повећава. У 3 димензије, вероватноћа се смањује за отприлике 34%.
Путања случајне шетње је збир локација које су посећене, које су занемарене док сшетњом не стигнемо на место. У једној димензији, путања су једноставно све тачке између минималне висине шетње која је постигнута и максимално (оба су, у просеку, по налогу √ н). У вишим димензијама скуп има занимљиве геометријске карактеристике. У ствари, један добија дискретни фрактал, то је скуп који показује стохастичко само-сличност на великим скалама, али се у малом обиму може посматрати "јаггеднесс" тако да произилази из мреже на којој се врши шетња. Две Лавлерове књиге наведене у даљем тексту су добар извор за ову тему.
Однос према Винеровом процесу[уреди | уреди извор]

Винеров процес је математичка формулација Брауновог кретања, случајног кретања тела у течностима веће специфичне густине од њега самог.
Винеров процес је повезан са случајном шетњом. Стохастички процес
за свако , где су то независне и идентични распоређене случајне променљиве са очекиваном вредношћу 0 и варијансом 1, за , тежи Винеровом процеесу. Конвергенција је дата Централном граничном теоремом.[12] Винеров процес у произвољној димензији је лимес случајне шетње у истој димензији.
Случајна шетња се може посматрати као дискретан фрактал, односно функција целобројних димензија 1, 2, ... Винеров процес је прави фрактал Хаусдорфове димензије 2.
Винеров процес шетње је инваријантан на ротације за произвољни угао, док је случајна шетња инваријантна само на ротације под правим углом, јер је дефинисана на целобројној решетки која сама не поседује инваријантност на остале ротације.
Гаусова случајна шетња[уреди | уреди извор]
Случајни шетња са бројем корака који варира према нормалној подели се користи као модел за реалне податке временских серија као што су финансијска тржишта. Црна-Сцхолес формула за цену је опција моделирања, на пример, користи Гаусову случајну шетњу као основну претпоставку
Овде, величина корака је инверзна кумулативној нормалној расподели где 0 ≤ z ≤ 1је равномерно распоређени случајни број, а μ и σ су средње и стандардне девијације нормалне дистрибуције, респективно.
Ако је μ различит од нуле, случајна шетња ће варирати око линеарног тренда. Обрнуто, ако је почетна вредност случајне шетње, очекивана вредност након н корака ће бити вс + нμ.
За посебан случај где је μ једнака нули, након н корака, расподелом удаљеност је Н (0, нσ2), где је Н () ознака за нормалну расподелу, н је број корака, и σ је инверзна кумулативна нормална дистрибуција као што је дато горе.
Доказати: Гаусова случајна шетња може да се посматрати као збир низа независних и идентично дистрибуираних случајних променљивих, Xи из обрнуте кумулативне нормалне дистрибуције са средњом једнаком нули и X обрнуте кумулативне нормалне дистрибуције:
- Z = ,
али имамо дистрибуцију за суму од две независно нормално дистрибуиране случајне променљиве, Z = X + Y, даје
- N(μX + μY, σ2X + σ2Y) (види овде).
У нашем случају, μX = μY = 0 и σ2X = σ2Y = σ2 доноси
- N(0, 2σ2)
По индукцији, за н корака имамо
- Z ~ N(0, nσ2).
За кораке дистрибуиране према било којој дистрибуцији са нулом на средини и коначне варијансе (не нужно само нормалне дистрибуције), корен средње квадратне удаљеност после н корака је
Али за Гаусову случајну шетњу, ово је само стандардна девијација дистрибуције превода удаљености након н корака. Дакле, ако је μ једнака нули, а од корена значи квадратна (РМС) превод удаљености је једна стандардна девијација, постоји 68,27% вероватноће да ће ефективна удаљеност након н корака пасти између± σ. Исто тако, постоји 50% вероватноће да ће удаљеност након н корака пасти између± 0.6745σ.
Аномална дифузија[уреди | уреди извор]
У поремећеним системима као што су порозна медија и фрактали не може бити пропорционална али може . Експонент се зове експонент аномалије дифузије и може бити већи или мањи од 2.[13]Аномалоус дифузија се такође може изразити као σr2 ~ Dtα где α је параметар аномалније.
Број различитих локација[уреди | уреди извор]
Број различитих локација које је посетио један случајни шетач је интензивно проучаван за квадратну и кубну летвицу и за фрактале.[14][15] Ова количина је корисна за анализу проблема хватања и кинетичких реакција. Такође је у вези са вибрационом густином стања, дифузијом реакције процеса и ширења популације у екологији.[16] Генерализација овог проблема на број различитих локација посетило је случајних шетача, , недавно је студирано за Д-димензионалне еуклидске решетке. Број различитих локација посећених од Н шетача у вези су са бројем различитих сајтова које посећује сваки шетач.
Апликације[уреди | уреди извор]

Следе неке апликације случајне шетње:
- У финансијској економији,"хипотеза случајна шетња" се користи за моделирање цена акција и других фактора. Емпиријска истраживања пронашла су нека одступања од овог теоријског модела, посебно у кратком року и дугорочним корелацијама. Погледајте цене акција.
- У популационе генетике, слободна шетња описује статистичке особине генетичког дрифта
- У физици, случајне шетње се користе као поједностављени модели физичког Бровновог кретања и дифузије, као што су случајно кретање молекула у течности и гасова. Видети на пример дифузионе ограничене агрегације. Такође у физици, случајне шетње и неке од интеракцији шетње играју улогу у квантној теорији поља.
- У математичкој екологији, случајне шетње се користе да опишу поједине покрете животиња, за емпиријске процесе подршке за биодиффусион, и повремено за моделирање динамике становништва.
- У физици полимера, случајна шетња описује идеалан ланац. То је најједноставнији модел проучавања полимера.
- У осталим областима математике, случајна шетња се користи за израчунавање решења Лапласове једначине, да процени хармоничну меру, и за различите конструкције у анализи и комбинаторици.
- У информатици, случајне шетње се користе за процену величине Веба. У Ворлд Виде Веб конференције 2006. године, бар-Иоссеф и др. објавили су своје налазе и алгоритме за исте.
- У слици сегментације, случајне шетње се користе за утврђивање налепнице (тј "објекат" или "позадина") да се држе сваког пиксела. Овај алгоритам се типично назива алгоритам сегментације случајне шетње.
У свим овим случајевима, случајна шетња је често замењена за Брауново кретање.
- У истраживању мозга, случајне шетње и ојачане случајне шетње се користе за моделирање каскаде неурона које пуцају у мозгу.
- У визији науке, очни заношење тежи да се понаша као случајна шетња. Према неким ауторима, фикатионал покрети ока у целини су такође добро описали случајну шетњу.[17]
- У психологији, случајне шетње објашњавају прецизно однос између времена потребног да се донесе одлука и вероватноће да ће одређена одлука да буде донета.
- Случајне шетње могу се користити за узорковање из државног простора који је непознат или веома велик, на пример, да изабере случајно страну са интернета, или за истраживање услова рада, случајни радник у датој земљи.
Када се овај последњи приступ користи у компјутерској науци познат је као уметање или МЦМЦ за кратко. Често, узорковање од неког компликованог државног простора такође омогућава да добијете вероватноће процене величине простора екипе. Процена стално велике матрице нуле и јединице је био први велики проблем за решити коришћењем овог приступа.
- Случајне шетње се такође користе за узорковање масивних онлајн графикона као што су они на онлајн друштвеним мрежама.
- У бежичном умрежавању, случајна шетња се користи за моделирање кретања чвора.
- Покретне бактерије које се ангажују у случајној шетњи.
- Случајне шетње се користе за моделирање коцкања.
- У физици, случајне шетње су у основи метод процене Ферми.
- На вебу, сајт Твиттер користи случајне шетње да предложи кога да пратиши[18]
Варијанте случајне шетње[уреди | уреди извор]
Велики број врста стохастичких процеса су сматрани да су слични чистим случајним шетњама, али где је дозвољено да једноставна структура буде уопштена. Чиста структура може бити окарактерисана корацима који дефинишу независне и идентично расподељене случајне променљиве.
Случајна шетња на графиконима[уреди | уреди извор]
Случајни хода дужине к бесконачно могућег графика Г са кореном 0 је стохастички процес са случајним променљивама тако да и је највиша тачка изабрана равномерно насумично из суседа .
Онда за број је вероватноћа да се случајна шетња од дужине к почетком у в завршава у В. Конкретно, ако је Г графикон са кореном 0, онда је вероватноћа да -корак слободне шетње враћа на 0.
Претпоставимо сада да наш град више није савршен квадрат мреже. Када наш пијаница достигне одређену раскрсницу он бира између различитих путева са једнаком вероватноћом. Стога, ако чвор има седам излаза пијанац ће ићи на сваки од њих са вероватноћом једне седмине. Ово је случајна шетња на графикону. Хоће ли наш пијаница доћи до своје куће? Испоставило се да под веома благим условима, одговор је увек да. На пример, ако су дужине свих блокова између А и Б (где су а и б било која два коначно позитивна броја), онда ће пијанац, готово сигурно, доћи до своје куће. Обратите пажњу да не претпостављамо да је графикон равни, односно град може да садржи тунеле и мостове. Један од начина да се докаже овај резултат јесте коришћење везе са електричним мрежама. Узмите мапу града и поставите једно ома отпорник на сваком блоку. Сада мери "отпор између тачке и бесконачности". Другим речима, изаберите неки број Р и предузети све тачке у електричну мрежу са удаљености веће од Р из наше тачке и послати их заједно. Ово је сада коначно електрична мрежа и можемо мерити отпор од наше тачке до жичаних тачака. Узмите Р до бесконачности. Граница се зове отпор између тачке и бесконачности. Испоставило се да је следеће тачно (елементарни доказ може се наћи у књизи Доиле и Снелл):
Теорема: график је пролазан ако и само ако је отпор између тачке и бесконачности коначан. Није важно ако је тачка изабрана ако је повезан график.
Другим речима, у пролазном систему, један само треба да превазиђе коначан отпор да се стигне до бесконачности из било које тачке. У повратном систему, отпор од било које тачке у бесконачности је бесконачан.
Ова карактеризација рецидива и пролазности је веома корисна, а посебно нам омогућава да анализирамо случај града састављен у равни са ограниченом раздаљином.
Случајна шетња на графу је веома посебан случај Марковог ланца. За разлику од општег Марковог ланца, случајна шетња на графикону има имовину која се зове време симетрија или понављање. Грубо говорећи, овај хотел, који се назива принцип детаљног баланса, значи да ће вероватноћа прећи дати пут у једном правцу или у другом и имамо веома једноставну везу између њих (ако је граф редовно, они су само једнаки). Ова некретнина има значајне последице.
Од 1980-их, много истраживања је извршено у циљу повезивања својства графикона до случајне шетње. Поред електричне мрежне конекције горе описане, постоје значајне везе са исопериметричним неједнакостима, функционалне неједнакости као што су Соболев и Поенкаре неједнакости и својства решења Лапласове једначине. Значајан део овог истраживања био је фокусиран на Цаилеием графовима коначно остварених група. На пример, доказ Даве Баиер и Перси Диацонис да 7 кундацима Схуффлес довољно да се меша шпил карата и на снази је резултат о случајној шетњи на групи СН, а доказ користи структуру групе у суштинском начину. У многим случајевима ови дискретни резултати преносе на, или су добијени од многострукости и група.
Добра референца за случајну шетњу на графиконима је онлине књига Алдоус и напуните. За групе види књигу Воесс.
Ако транзиција кернелаје сама случајна (на основу животне \ омега) онда се случајна шетња зове "случајна шетња по случајном окружењу". Када закон случајне шетње укључује случајности \ омега, закон се зове аннеалед закон; С друге стране, ако \ омега се сматра фиксним, закон се назива гаси закон. Погледајте књигу Хугхес или предавање Зеитоуни.
Можемо да размишљамо о избору сваке могуће предност са истом вероватноћом као максималном локалном несигурношћу (ентропија) . Ми такође можемо то урадити на глобалном нивоу - у максималној ентропији случајне шетње (МЕРВ) желимо да сви путеви буду подједнако вероватни, или другим речима: за свака два вертекес, сваки пут дате дужине је подједнако вероватан. Ова случајна шетња има много јаче особине локализације.
Полу-интерагујућа случајна шетња[уреди | уреди извор]
Постоји велики број занимљивих модела случајних путања у којој сваки корак зависи од прошлости у компликованом начину. Сви су сложенији за аналитичко решавање од уобичајеног случајног корака; даље, понашање било ког модела случајне шетње је добити помоћу рачунара. Примери укључују:
- Полу-избегавајућа шетња (Мадрас и Сладе 1996)).[19]
Полу-избегавајућа шетња дужине н о з ^ д је случајна п Н-корак који почиње у пореклу, чини прелазе само између суседних локација у з ^ д, никада не посећује сајт, и равномерно је изабран међу свим тим путевима. У две димензије, до услед само-хватање, типична само-избегавајућа шетња је врло кратка, док у вишу димензију расте изнад свих граница. Овај модел се често користи у физици полимера (од 1960)
- Избрисана петља случајне шетње (Gregory Lawler).[20][21]
- Ојачана случајна шетња (Robin Pemantle 2007).[22]
- Процес истраживања.
- Мултиагент случајне шетње.[23]
Дуге колерацијске шетње[уреди | уреди извор]
Дуге корелацијске временске серије се могу наћи у многим биолошким, климатских и економских системима..
- Heartbeat records[24]
- Non-coding DNA sequences[25]
- Volatility time series of stocks[26]
- Temperature records around the globe[27]
Види још[уреди | уреди извор]
Референце[уреди | уреди извор]
- ^ Pearson, K.
- ^ Van Kampen N. G., Stochastic Processes in Physics and Chemistry, revised and enlarged edition (North-Holland, Amsterdam) 1992.
- ^ Redner S., A Guide to First-Passage Process (Cambridge University Press. Cambridge, UK) 2001.
- ^ Goel N. W. and Richter-Dyn N., Stochastic Models in Biology (Academic Press, New York) 1974.
- ^ Doi M. and Edwards S. F., The Theory of Polymer Dynamics (Clarendon Press, Oxford) 1986
- ^ De Gennes P. G., Scaling Concepts in Polymer Physics (Cornell University Press, Ithaca and London) 1979.
- ^ Risken H., The Fokker–Planck Equation (Springer, Berlin) 1984.
- ^ Weiss, George H. (1994), Aspects and Applications of the Random Walk, Random Materials and Processes, North-Holland Publishing Co., Amsterdam. 1905. ISBN 978-0-444-81606-1., MR 1280031.
- ^ Cox D. R., Renewal Theory (Methuen, London) 1962.
- ^ Random Walk-1-Dimensional - from Wolfram MathWorld
- ^ M. Kotani, T. Sunada (2006).
- ^ Steven Lalley, Mathematical Finance 345 Lecture 5: Brownian Motion (2001)
- ^ D. Ben-Avraham and S. Havlin, Diffusion and Reactions in Fractals and Disordered Systems Архивирано на сајту Wayback Machine (4. октобар 2011), Cambridge University Press, 2000.
- ^ Weiss, George H.; Rubin, Robert J. (1982).
- ^ Blumen, A.; Klafter, J.; Zumofen, G. (1986).
- ^ Skellam, J. G. (1951).
- ^ Ralf Engbert, Konstantin Mergenthaler, Petra Sinn, and Arkady Pikovsk: "An integrated model of fixational eye movements and microsaccades"
- ^ Pankaj Gupta, Ashish Goel, Jimmy Lin, Aneesh Sharma, Dong Wang, and Reza Bosagh Zadeh WTF: The who-to-follow system at Twitter, Proceedings of the 22nd international conference on World Wide Web
- ^ Neal Madras and Gordon Slade (1996), The Self-Avoiding Walk, Birkhäuser Boston.
- ^ Gregory Lawler (1996).
- ^ Gregory Lawler, Conformally Invariant Processes in the Plane, book.ps.
- ^ Robin Pemantle (2007), A survey of random processes with reinforcement.
- ^ Alamgir, M and von Luxburg, U (2010).
- ^ C.-K. Peng, J. Mietus, J. M. Hausdorff, S. Havlin, H. E. Stanley, A. L. Goldberger (1993).
- ^ C.-K. Peng, S. V. Buldyrev, A. L. Goldberger, S. Havlin, F. Sciortino, M. Simons, H. E. Stanley (1992).
- ^ Y. Liu, P. Cizeau, M. Meyer, C.-K. Peng, H. E. Stanley (1997).
- ^ E. Koscielny-Bunde, A. Bunde, S. Havlin, H. E. Roman, Y. Goldreich, H.-J. Schellenhuber (1998).
Литература[уреди | уреди извор]
- Stein, Rolf Alfred (1972). Tibetan Civilization. Stanford University Press. ISBN 978-0-8047-0901-9.
- Aldous, David; Fill, Jim, Reversible Markov Chains and Random Walks on Graphs, https://web.archive.org/web/20040921020230/http://stat-www.berkeley.edu/users/aldous/RWG/book.html
- Ben-Avraham D.; Havlin S., Diffusion and Reactions in Fractals and Disordered Systems Архивирано на сајту Wayback Machine (4. октобар 2011), Cambridge University Press, 2000.
- Doyle, Peter G.; Snell, J. Laurie (1984). Random Walks and Electric Networks. Carus Mathematical Monographs 22. Mathematical Association of America. arXiv:math.PR/0001057. ISBN 978-0-88385-024-4. Спољашња веза у
|publisher=(помоћ)MR 920811 - Feller, William (1968). An Introduction to Probability Theory and its Applications. I. ISBN 978-0-471-25708-0.
- Hughes, Barry D. (1996). Random Walks and Random Environments. Oxford University Press. ISBN 978-0-19-853789-2.
- Mackenzie, Dana, "Taking the Measure of the Wildest Dance on Earth", Science, Vol. 290, 8 December 2000.
- Norris, James (1998). Markov Chains. Cambridge University Press. ISBN 978-0-521-63396-3.
- Pólya G.(1921), "Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Strassennetz", Mathematische Annalen, 84(1-2):149–160, March 1921.
- Révész, Pal (2013). Random Walk in Random and Non-random Environments (3rd изд.). World Scientific Pub Co. ISBN 978-981-4447-50-8.
- Weiss G. Aspects and Applications of the Random Walk, North-Holland, 1994.
- Toshikazu Sunada (2012), Topological Crystallography --With a View Towards Discrete Geometric Analysis--, Surveys and Tutorials in the Applied Mathematical Sciences, Vol. 6, Springer

















![{\displaystyle P[S_{0}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4fec1fd8784c3de7c8b113f7ff728db75c8f584)
![{\displaystyle 2P[S_{1}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c61317a7c5e847ee2756e0a746abee7bdd9da12)
![{\displaystyle 2^{2}P[S_{2}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9583c3e61f6b6739502821af6cb79fae46f22e)
![{\displaystyle 2^{3}P[S_{3}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/283a77c450ba9f63e54a01a94fb9cec8e8ee07b8)
![{\displaystyle 2^{4}P[S_{4}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/208950bbe9ff3b0dd09b94b35dd390d3ddefea15)
![{\displaystyle 2^{5}P[S_{5}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b86e6675acd3df11dbd6fd80d3e1c0b10e3b6bf)























