Гама-функција
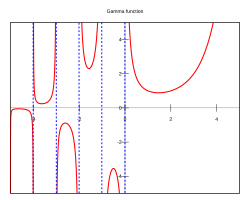
У математици, гама-функција је функција дефинисана несвојственим интегралом:
Из парцијалне интеграције и израчунавања интеграла за , добија се израз
који проширује појам факторијелa[1] на комплексне бројеве.[2]
Дефиниција[уреди | уреди извор]
Гама-функција дефинисана је несвојственим интегралом[3][4] за комплексне бројеве за које је на следећи начин:
Другим речима, гама-функција је Мелинова трансформација функције . Парцијалним интеграљењем се показује следеће њено основно својство:
Како је , комбиновањем ове и претходне релације добија се:
за све природне бројеве n.
Са друге стране, формулисана у облику
- ,
она даје аналитичко продужење почетно дефинисаној -функцији до полуравни , са полом у , затим до полуравни , са још једним полом у , итд. Тако се -функција продужује до мероморфне функције, дефинисане за све комплексне бројеве осим полова у непозитивним целим бројевима Под -функцијом се, по правилу, подразумева овако дефинисано продужење.
Основна својства[уреди | уреди извор]
Гама-функција није елементарна функција, али су њена својства веома добро истражена због њене повезаности са факторијелом и примене у теорији бројева. Међу најважнијима особинама Гама-функције су функционална једначина
и Лежандрова дупликациона формула
Гама-функција нема нула. У тачкама , где је ненегативан цео број, гама-функција има пол реда 1 са остатком ; њено понашање у околини полова одређено је функционалном једначином.
За велике , вредности даје са великом прецизношћу Стирлингова апроксимациона формула:
За све z где је гама-функција дефинисана, важи и следећи бесконачан производ

где је γ Ојлерова константа, који се добија као Вајерштрасов производ функције , која је цела јер гама-функција нема нула, и реда 1 према Стрилинговој формули. Некад се заправо за дефиницију гама-функције узима овај производ, или неки од еквивалентних облика
Ваљда најпознатија вредност гама-функције за нецелобројне вредности аргумента је , што се може видети нпр. коришћењем дупликационе формуле. Овај резултат даје и вредност такозваног интеграла вероватноће
који је од изузетне важности у вероватноћи и статистици. Тако једноставне формуле нису познате већ нпр. за (). За и је познато да су трансцендентни, као и . Такође, .
Веома ретко користе се и алтернативне ознаке и . Тако је , док је функција π цела.
Према Бор-Молеруповој теореми, гама-функција је једина логаритамски конвексна функција која проширује факторијел на све позитивне бројеве.
Дупликациона формула је специјални случај следеће Гаусове теореме о производу:
Гама-функција је од изузетног значаја у математичкој анализи, вероватноћи и статистици, теорији бројева, комбинаторици и другим областима математике, те у физици, техници и другим областима.
Историјат[уреди | уреди извор]
Гама-функцију први је посматрао и изучавао Леонард Ојлер, који је доказао и функционалну једначину. Неки је називају и Ојлеровим интегралом друге врсте. Ознаку је увео Адријан-Мари Лежандр, коме дугујемо дупликациону формулу.
Индијски математичар Рамануџан доказао је низ фасцинантних идентитета са гама-функцијом.
Уопштења и везе са другим функцијама[уреди | уреди извор]
У интегралу којим се дефинише -функција, границе интеграције су фиксиране. Често је пожељно посматрати такав интеграл у којем је доња или горња граница променљива (често у зависности од z), тако се добија непотпуна гама-функција. Логаритамски извод понекад се назива и дигама-функцијом. У статистици и другде је од значаја вишедимензиона гама-функција.
Са апстрактне алгебарске тачке гледишта, интеграл којим се дефинише гама-функција представља конволуцију мултипликативног карактера поља реалних бројева са једним фиксираним адитивним карактером тог поља. На тај начин своју гама-функцију има, на пример, свако алгебарско бројно поље, нормирано локално поље, итд. У теорији бројева, такве гама-функције део су функционалних једначина Л-функција. Види још Риманова зета-функција.
Апроксимације[уреди | уреди извор]

Комплексне вредности гама функције могу се израчунати нумерички са произвољном прецизношћу користећи Стирлингову апроксимацију или Ланцошову апроксимацију.
Гама функција се може израчунати са фиксном прецизношћу за применом парцијалне интеграције у Ојлеровом интегралу. За било који позитивни број x може се написати гама функција
Кад је Re(z) ∈ [1,2] и , апсолутна вредност задњег интеграла је мања од . Одабиром довољно великог , овај последњи израз може се учинити мањим од за било коју жељену вредност . Тако се гама функција може проценити на бита прецизности са горенаведеном серијом.
Е.А. Каратсуба је конструисао брз алгоритам за израчунавање Ојлерове гама функције за било који алгебарски аргумент (укључујући и рационални).[5][6][7]
За аргументе који су целобројни умношци од 1/24, гама функција се такође може брзо проценити коришћењем аритметичко-геометријских средњих вредности итерација (погледајте посебне вредности гама функције и Borwein & Zucker (1992)).
Апликације[уреди | уреди извор]
Један аутор описује гама функцију као „Аргументирано, најчешћу специјалну функцију, или најмање 'посебну' од њих. Друге трансценденталне функције […] називају се 'посебне', јер бисте неке од њих могли избећи држањем подаље од многих специјализованих математичких тема. Са друге стране, гама функцију y = Γ(x) је најтеже избећи.”[8]
Види још[уреди | уреди извор]
Референце[уреди | уреди извор]
- ^ Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1988). Concrete Mathematics. Reading, MA: Addison-Wesley. стр. 111. ISBN 0-201-14236-8.
- ^ О Гама функцији, белешке са предавања 1995. године Архивирано на сајту Wayback Machine (2. мај 2014), Универзитет у Олбани, Њујорк, Приступљено: 2.5.2014.
- ^ Buck, R. Creighton (1965). Advanced Calculus (2nd изд.). McGraw-Hill. стр. 133–134.
- ^ Spiegel, Murray R. (1963). Schaum's Outline of Theory and Problems of Advanced Calculus. McGraw-Hill. стр. 260. ISBN 0-07-060229-8.
- ^ E.A. Karatsuba, Fast evaluation of transcendental functions. Probl. Inf. Transm. Vol.27, No.4, pp. 339–360 (1991).
- ^ E.A. Karatsuba, On a new method for fast evaluation of transcendental functions. Russ. Math. Surv. Vol.46, No.2, pp. 246–247 (1991).
- ^ E.A. Karatsuba "Fast Algorithms and the FEE Method"
- ^ Michon, G. P. "Trigonometry and Basic Functions Архивирано 2010-01-09 на сајту Wayback Machine". Numericana. Retrieved May 5, 2007.
Литература[уреди | уреди извор]
- Abramowitz, Milton; Stegun, Irene A., ур. (1972). „Chapter 6”. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover.
- Andrews, G. E.; Askey, R.; Roy, R. (1999). „Chapter 1 (Gamma and Beta functions)”. Special Functions. New York: Cambridge University Press. ISBN 978-0-521-78988-2.
- Artin, Emil (2006). „The Gamma Function”. Ур.: Rosen, Michael. Exposition by Emil Artin: a selection. History of Mathematics. 30. Providence, RI: American Mathematical Society.
- Askey, R.; Roy, R. (2010), „Гама-функција”, Ур.: Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- Birkhoff, George D. (1913). „Note on the gamma function”. Bull. Amer. Math. Soc. 20 (1): 1—10. MR 1559418. doi:10.1090/s0002-9904-1913-02429-7.
- Böhmer, P. E. (1939). Differenzengleichungen und bestimmte Integrale [Differential Equations and Definite Integrals]. Leipzig: Köhler Verlag.
- Davis, Philip J. (1959). „Leonhard Euler's Integral: A Historical Profile of the Gamma Function”. American Mathematical Monthly. 66: 849—869. doi:10.2307/2309786.
- Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007). „Section 6.1. Gamma Function”. Numerical Recipes: The Art of Scientific Computing (3rd изд.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. Архивирано из оригинала 27. 10. 2021. г. Приступљено 16. 12. 2018.
- Rocktäschel, O. R. (1922). Methoden zur Berechnung der Gammafunktion für komplexes Argument [Methods for Calculating the Gamma Function for Complex Arguments]. Dresden: Technical University of Dresden.
- Temme, Nico M. (1996). Special Functions: An Introduction to the Classical Functions of Mathematical Physics. New York: John Wiley & Sons. ISBN 978-0-471-11313-3.
- Whittaker, E. T.; Watson, G. N. (1927). A Course of Modern Analysis. Cambridge University Press. ISBN 978-0-521-58807-2.
- Amdeberhan, T.; Coffey, Mark W.; Espinosa, Olivier; Koutschan, Christoph; Manna, Dante V.; Moll, Victor H. (2011). „Integrals of powers of loggamma”. Proc. Amer. Math. Soc. 139 (2): 535—545. doi:10.1090/S0002-9939-2010-10589-0
 .
. - Borwein, J.; Bailey, D. H.; Girgensohn, R. (2003). Experimentation in Mathematics. A. K. Peters. стр. 133. ISBN 978-1-56881-136-9.
- Davis, P. J. (1959). „Leonhard Euler's Integral: A Historical Profile of the Gamma Function”. American Mathematical Monthly. 66 (10): 849—869. JSTOR 2309786. doi:10.2307/2309786. Архивирано из оригинала 07. 11. 2012. г. Приступљено 3. 12. 2016.
- Remmert, R. (2006). Classical Topics in Complex Function Theory. Превод: Kay, L. D. Springer. ISBN 978-0-387-98221-2.
- Knuth, D. E. (1997). The Art of Computer Programming, Volume 1 (Fundamental Algorithms). Addison-Wesley.
Спољашње везе[уреди | уреди извор]
- NIST Digital Library of Mathematical Functions:Gamma function
- Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function. In PostScript and HTML formats.
- C++ reference for std::tgamma
- Examples of problems involving the gamma function can be found at Exampleproblems.com.
- Hazewinkel Michiel, ур. (2001). „Gamma function”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104.
- Wolfram gamma function evaluator (arbitrary precision)
- „Gamma”. Wolfram Functions Site.
- Volume of n-Spheres and the Gamma Function at MathPages









































![{\displaystyle \operatorname {Re} (z)\in [1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bf2e1f1d1d9be1282a2cc03b29b1a8d048fcca6)





