Четвороугао — разлика између измена
м Враћене измене корисника 77.243.25.11 (разговор) на последњу измену корисника Smilutin ознака: враћање |
. |
||
| Ред 1: | Ред 1: | ||
{{Short description|Полигон са четири стране и четири угла}} |
|||
{{Инфокутија многоугао |
{{Инфокутија многоугао |
||
| име = Четвороугао |
| име = Четвороугао |
||
| Ред 14: | Ред 15: | ||
}} |
}} |
||
'''Четвороугао''' је у геометрији у равни затворени геометријски облик кога окружују четири [[дуж]]и спојене у четири темена.<ref>{{cite book | last = Heath | first = Thomas L. | authorlink = T. L. Heath | title = The Thirteen Books of Euclid's Elements | edition = 2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] | year = 1956 | publisher = Dover Publications | location = New York }} In 3 vols.: vol. 1 {{ISBN|0-486-60088-2}}, vol. 2 {{ISBN|0-486-60089-0}}, vol. 3 {{ISBN|0-486-60090-4}}</ref> Формална дефиниција четвороугла каже да је четвороугао многоугао који има четири темена. Сваки четвороугао има тачно две дијагонале. Дијагонала је дуж која спаја два несуседна темена. Други назив за општи четвороугао је '''трапезоид'''. Трапезоиди (као нпр. делтоид) немају паралелне странице. |
'''Четвороугао''' је у [[Euclidean geometry|геометрији]] у равни затворени геометријски облик кога окружују четири [[дуж]]и спојене у четири темена.<ref>{{cite book | last = Heath | first = Thomas L. | authorlink = T. L. Heath | title = The Thirteen Books of Euclid's Elements | edition = 2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] | year = 1956 | publisher = Dover Publications | location = New York }} In 3 vols.: vol. 1 {{ISBN|0-486-60088-2}}, vol. 2 {{ISBN|0-486-60089-0}}, vol. 3 {{ISBN|0-486-60090-4}}</ref> Формална дефиниција четвороугла каже да је четвороугао многоугао који има четири темена. Сваки четвороугао има тачно две дијагонале. Дијагонала је дуж која спаја два несуседна темена. Други назив за општи четвороугао је '''трапезоид'''. Трапезоиди (као нпр. делтоид) немају паралелне странице. |
||
Реч „квадрилатералан” је изведена из латинских речи -{''quadri''}-, варијанте речи четири, и -{''latus''}-, са значењем „страна”. Квадрилатерали су [[simple polygon|једноставни]] (без самопресецања) или [[complex polygon|комплексни]] (самопресецајући), који се такође називају укрштеним. Једноставни четвороугли су или [[convex polygon|конвексни]] или [[concave polygon|конкавни]]. |
Реч „квадрилатералан” је изведена из латинских речи -{''quadri''}-, варијанте речи четири, и -{''latus''}-, са значењем „страна”. Квадрилатерали су [[simple polygon|једноставни]] (без самопресецања) или [[complex polygon|комплексни]] (самопресецајући), који се такође називају укрштеним. Једноставни четвороугли су или [[convex polygon|конвексни]] или [[concave polygon|конкавни]]. Четвороугао са врховима <math>A</math>, <math>B</math>, <math>C</math> и <math>D</math> се понекад означава као <math>\square ABCD</math>.<ref name=":0">{{Cite web|title=Quadrilaterals - Square, Rectangle, Rhombus, Trapezoid, Parallelogram|url=https://www.mathsisfun.com/quadrilaterals.html|access-date=2020-09-02|website=Mathsisfun.com}}</ref> |
||
[[Internal and external angle|Унутрашњи углови]] једноставног (и планарног) четвороугла -{''ABCD''}- имају суму од 360 [[Степен (угао)|угаоних степени]], односно <math>\angle A+\angle B+\angle C+\angle D=360^{\circ}.</math> Ово је посебан случај формуле суме унутрашњих углова (-{''n''}- − 2) × 180°. Сви четвороугаоници без самоукрштања [[Теселација|постављају]] раван формирану поновљеном ротацијом око средишта њихових ивица. |
[[Internal and external angle|Унутрашњи углови]] једноставног (и планарног) четвороугла -{''ABCD''}- имају суму од 360 [[Степен (угао)|угаоних степени]],<ref name=":0" /> односно <math>\angle A+\angle B+\angle C+\angle D=360^{\circ}.</math> Ово је посебан случај формуле суме унутрашњих углова (-{''n''}- − 2) × 180°.<ref>{{Cite web|url=https://www.cuemath.com/geometry/sum-of-angles-in-a-polygon/|title=Sum of Angles in a Polygon|website=Cuemath|access-date=22 June 2022}}</ref> Сви четвороугаоници без самоукрштања [[Теселација|постављају]] раван формирану поновљеном ротацијом око средишта њихових ивица.<ref>{{citation|last=Martin|first=George Edward|doi=10.1007/978-1-4612-5680-9|isbn=0-387-90636-3|mr=718119|at=Theorem 12.1, page 120|publisher=Springer-Verlag|series=Undergraduate Texts in Mathematics|title=Transformation geometry|url=https://books.google.com/books?id=gevlBwAAQBAJ&pg=PA120|year=1982}}</ref> |
||
== Подела четвороуглова == |
== Подела четвороуглова == |
||
Четвороуглови се пре свега деле на [[Многоугао#Конвексност|конвексне]] и неконвексне. Неконвексни се деле на четвороуглове са и без самопресека. Потребан и довољан услов да четвороугао буде конвексан је да се дијагонале четвороугла секу.<ref name="oed">{{cite book|title=A New English Dictionary on Historical Principles: Founded Mainly on the Materials Collected by the Philological Society|author=James A. H. Murray|volume=X|date=1926|url=https://archive.org/details/oedxaarch/page/n296/mode/1up|page=286 (Trapezium)|publisher=Clarendon Press at Oxford|quote=With Euclid (c 300 B.C.) τραπέζιον included all quadrilateral figures except the square, rectangle, rhombus, and rhomboid; into the varieties of trapezia he did not enter. But Proclus, who wrote Commentaries on the First Book of Euclid's Elements A.D. 450, retained the name τραπέζιον only for quadrilaterals having two sides parallel, subdividing these into the τραπέζιον ἰσοσκελὲς, isosceles trapezium, having the two non-parallel sides (and the angles at their bases) equal, and σκαληνὸν τραπέζιον, scalene trapezium, in which these sides and angles are unequal. For quadrilaterals having no sides parallel, Proclus introduced the name τραπέζοειδὲς TRAPEZOID. This nomenclature is retained in all the continental languages, and was universal in England till late in the 18th century, when the application of the terms was transposed, so that the figure which Proclus and modern geometers of other nations call specifically a trapezium (F. trapèze, Ger. trapez, Du. trapezium, It. trapezio) became with most English writers a trapezoid, and the trapezoid of Proclus and other nations a trapezium. This changed sense of trapezoid is given in Hutton's Mathematical Dictionary, 1795, as ‘sometimes’ used -- he does not say by whom; but he himself unfortunately adopted and used it, and his Dictionary was doubtless the chief agent in its diffusion. Some geometers however continued to use the terms in their original senses, and since c 1875 this is the prevalent use.}}</ref><ref name="ConwayBurgiel2016">{{cite book|last1=Conway|first1=John H.|last2=Burgiel|first2=Heidi|last3=Goodman-Strauss|first3=Chaim|title=The Symmetries of Things|url=https://books.google.com/books?id=Drj1CwAAQBAJ&pg=PA286|date=5 April 2016|publisher=CRC Press|isbn=978-1-4398-6489-0|pages=286}}</ref> |
|||
Четвороуглови се пре свега деле на [[Многоугао#Конвексност|конвексне]] и неконвексне. Неконвексни се деле на четвороуглове са и без самопресека. Потребан и довољан услов да четвороугао буде конвексан је да се дијагонале четвороугла секу. |
|||
Основна подела конвексних четвороуглова је према броју парова паралелних страница. Приметимо да суседне странице [[многоугао|многоугла]] не могу бити паралелне, јер се праве које их садрже секу у темену многоугла. Сваке две странице троугла су суседне, па наведена подела није била применљива на [[Троугао|троуглове]]. Конвексан четвороугао који има један пар паралелних страница зовемо [[трапез (геометрија)|трапез]], а онај који има два пара паралелних страница зовемо [[паралелограм]]. |
Основна подела конвексних четвороуглова је према броју парова паралелних страница. Приметимо да суседне странице [[многоугао|многоугла]] не могу бити паралелне, јер се праве које их садрже секу у темену многоугла. Сваке две странице троугла су суседне, па наведена подела није била применљива на [[Троугао|троуглове]]. Конвексан четвороугао који има један пар паралелних страница зовемо [[трапез (геометрија)|трапез]],<ref>http://www.mathopenref.com/trapezoid.html Mathopenref definition</ref><ref>A. D. Gardiner & C. J. Bradley, ''Plane Euclidean Geometry: Theory and Problems'', UKMT, 2005, p. 34.</ref> а онај који има два пара паралелних страница зовемо [[паралелограм]]. |
||
Напомена. У литератури постоји извесно неслагање по питању тога да ли је скуп паралелограма подскуп скупа трапеза или су то два дисјунктна [[Скуп|скупа]]. Ствар је у различитим интерпретацијама [[Дефиниција|дефиниције]] трапеза. Док једни сматрају да је трапез сваки четвороугао који има бар један пар паралелних страница, други преферирају да трапезом називају само онај четвороугао који има тачно један пар паралелних страница. |
Напомена. У литератури постоји извесно неслагање по питању тога да ли је скуп паралелограма подскуп скупа трапеза или су то два дисјунктна [[Скуп|скупа]]. Ствар је у различитим интерпретацијама [[Дефиниција|дефиниције]] трапеза. Док једни сматрају да је трапез сваки четвороугао који има бар један пар паралелних страница, други преферирају да трапезом називају само онај четвороугао који има тачно један пар паралелних страница. |
||
| Ред 38: | Ред 39: | ||
Општи трапез има још три специјална подслучаја: |
Општи трапез има још три специјална подслучаја: |
||
* [[Паралелограм]] или ромбоид, |
* [[Паралелограм]] или ромбоид, |
||
* [[Правоугли трапез]], коме је бар један (па онда и њему суплементан) угао прав, |
* [[Правоугли трапез]], коме је бар један (па онда и њему суплементан) угао прав,<ref>{{Cite web|url=https://www.basic-mathematics.com/types-of-quadrilaterals.html|title=Types of Quadrilaterals|website=Basic-mathematics.com}}</ref> |
||
* [[Једнакокраки трапез]], који има једнаке углове на основици или једнаке дијагонале, а тиме и једнаке краке. Овај трапез је такође тетивни четвороугао. |
* [[Једнакокраки трапез]], који има једнаке углове на основици или једнаке дијагонале, а тиме и једнаке краке. Овај трапез је такође тетивни четвороугао. |
||
| Ред 44: | Ред 45: | ||
Паралелограм има два специјална случаја: |
Паралелограм има два специјална случаја: |
||
* [[Ромб]] је четвороугао коме су све странице једнаке, а специјалан је случај паралелограма и делтоида, |
* [[Ромб]] је четвороугао коме су све странице једнаке, а специјалан је случај паралелограма и делтоида,<ref>{{cite web|url=http://www.cimt.plymouth.ac.uk/resources/topics/art002.pdf|title=CIMT - Page no longer available at Plymouth University servers|website=www.cimt.plymouth.ac.uk|url-status=dead|archive-url=https://web.archive.org/web/20140514200449/http://www.cimt.plymouth.ac.uk/resources/topics/art002.pdf|archive-date=2014-05-14}}</ref> |
||
* [[Правоугаоник]] је четвороугао коме су сви углови (или бар три) прави и такође је специјалан случај паралелограма. Ако прихватамо дефиницију трапеза која обухвата паралелограме, онда је правоугаоник осим тога специјалан случај и једнакокраког и правоуглог трапеза. |
* [[Правоугаоник]] је четвороугао коме су сви углови (или бар три) прави и такође је специјалан случај паралелограма. Ако прихватамо дефиницију трапеза која обухвата паралелограме, онда је правоугаоник осим тога специјалан случај и једнакокраког и правоуглог трапеза. |
||
| Ред 66: | Ред 67: | ||
== Референце == |
== Референце == |
||
{{reflist}} |
{{reflist}} |
||
== Литература == |
|||
{{Refbegin|30em}} |
|||
* {{citation|title=Generalizations of Kempe's Universality Theorem|type=Master's thesis|url=http://web.mit.edu/tabbott/www/papers/mthesis.pdf|publisher=[[Масачусетски институт технологије|Massachusetts Institute of Technology]]|year=2008|first=Timothy Good|last=Abbott|contribution=3.1.2 Contraparallelograms|pages=34–36}} |
|||
* {{citation |
|||
| last1 = Coxeter | first1 = H. S. M. | author1-link = Harold Scott MacDonald Coxeter |
|||
| last2 = Longuet-Higgins | first2 = M. S. | author2-link = Michael S. Longuet-Higgins |
|||
| last3 = Miller | first3 = J. C. P. | author3-link = J. C. P. Miller |
|||
| bibcode = 1954RSPTA.246..401C |
|||
| doi = 10.1098/rsta.1954.0003 |
|||
| journal = Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences |
|||
| jstor = 91532 |
|||
| mr = 0062446 |
|||
| pages = 401–450 |
|||
| title = Uniform polyhedra |
|||
| volume = 246 |
|||
| year = 1954| issue = 916 | s2cid = 202575183 }} |
|||
* {{citation |
|||
| last1 = Alsina | first1 = Claudi |
|||
| last2 = Nelsen | first2 = Roger B. |
|||
| isbn = 978-1-4704-5312-1 |
|||
| location = Providence, Rhode Island |
|||
| mr = 4286138 |
|||
| page = 212 |
|||
| publisher = MAA Press and American Mathematical Society |
|||
| series = The Dolciani Mathematical Expositions |
|||
| title = A Cornucopia of Quadrilaterals |
|||
| url = https://books.google.com/books?id=CGDSDwAAQBAJ&pg=PA212 |
|||
| volume = 55 |
|||
| year = 2020}} |
|||
* {{citation |
|||
| last = Cundy | first = H. Martyn | author-link = Martyn Cundy |
|||
| date = March 2005 |
|||
| doi = 10.1017/s0025557200176855 |
|||
| issue = 514 |
|||
| journal = [[The Mathematical Gazette]] |
|||
| pages = 89–93 |
|||
| title = 89.23 The lemniscate of Bernoulli |
|||
| volume = 89| s2cid = 125521872 }} |
|||
* {{citation |
|||
| last1 = Begalla | first1 = Engjëll |
|||
| last2 = Perucca | first2 = Antonella |
|||
| hdl = 10993/43232 |
|||
| publisher = University of Luxembourg |
|||
| title = The ABCD of cyclic quadrilaterals |
|||
| journal = Uitwiskeling |
|||
| year = 2020}} |
|||
* {{citation |
|||
| last = Dijksman | first = E. A. |
|||
| isbn = 9780521208413 |
|||
| page = 203 |
|||
| publisher = Cambridge University Press |
|||
| title = Motion Geometry of Mechanisms |
|||
| url = https://books.google.com/books?id=wwY9AAAAIAAJ&pg=PA203 |
|||
| year = 1976}} |
|||
* {{citation |
|||
| last1 = Demaine | first1 = Erik | author1-link = Erik Demaine |
|||
| last2 = O'Rourke | first2 = Joseph | author2-link = Joseph O'Rourke (professor) |
|||
| doi = 10.1017/CBO9780511735172 |
|||
| isbn = 978-0-521-85757-4 |
|||
| mr = 2354878 | pages = 32–33 |
|||
| publisher = Cambridge University Press |
|||
| title = Geometric Folding Algorithms |
|||
| year = 2007}} |
|||
* {{citation |
|||
| last1 = Grebenikov | first1 = Evgenii A. |
|||
| last2 = Ikhsanov | first2 = Ersain V. |
|||
| last3 = Prokopenya | first3 = Alexander N. |
|||
| contribution = Numeric-symbolic computations in the study of central configurations in the planar Newtonian four-body problem |
|||
| doi = 10.1007/11870814_16 |
|||
| location = Berlin |
|||
| mr = 2279793 |
|||
| pages = 192–204 |
|||
| publisher = Springer |
|||
| series = Lecture Notes in Comput. Sci. |
|||
| title = Computer algebra in scientific computing |
|||
| volume = 4194 |
|||
| year = 2006}} |
|||
* {{citation |
|||
| last = Glaeser | first = Georg |
|||
| contribution = Antiparallelograms; It does not always have to be a uniform rotation ... |
|||
| doi = 10.1007/978-3-030-61398-3 |
|||
| pages = 428–429 |
|||
| publisher = Springer International Publishing |
|||
| title = Geometry and its Applications in Arts, Nature and Technology |
|||
| year = 2020| isbn = 978-3-030-61397-6 |
|||
}} |
|||
* {{citation |
|||
| last = De Villiers | first = Michael |
|||
| hdl = 10520/EJC175721 |
|||
| issue = 18 |
|||
| journal = Learning and Teaching Mathematics |
|||
| pages = 23–28 |
|||
| title = Slaying a geometrical 'monster': finding the area of a crossed quadrilateral |
|||
| volume = 2015 |
|||
| year = 2015}} |
|||
* {{citation |
|||
| last = Muirhead | first = R. F. | author-link = Robert Franklin Muirhead |
|||
| date = February 1901 |
|||
| doi = 10.1017/s0013091500032892 |
|||
| journal = Proceedings of the Edinburgh Mathematical Society |
|||
| pages = 70–72 |
|||
| title = Geometry of the isosceles trapezium and the contra-parallelogram, with applications to the geometry of the ellipse |
|||
| volume = 20| doi-access = free |
|||
}} |
|||
* {{citation |
|||
| last = Norton | first = Robert L. |
|||
| isbn = 978-0-07-121496-4 |
|||
| page = 51 |
|||
| publisher = McGraw-Hill Professional |
|||
| title = Design of Machinery |
|||
| year = 2003}} |
|||
* {{citation |
|||
| last1 = Bryant | first1 = John |
|||
| last2 = Sangwin | first2 = Christopher J. |
|||
| contribution = 3.3 The Crossed Parallelogram |
|||
| contribution-url = https://books.google.com/books?id=iIN_2WjBH1cC&pg=PA54 |
|||
| isbn = 978-0-691-13118-4 |
|||
| pages = 54–56 |
|||
| publisher = Princeton University Press |
|||
| title = How Round Is Your Circle? Where Engineering and Mathematics Meet |
|||
| title-link = How Round Is Your Circle |
|||
| year = 2008}} |
|||
* {{citation |
|||
| last = Sossinsky | first = Alexey |
|||
| contribution = Configuration spaces of planar linkages |
|||
| location = Zürich |
|||
| mr = 3618193 |
|||
| pages = 335–373 |
|||
| publisher = European Mathematical Society |
|||
| series = IRMA Lectures in Mathematics and Theoretical Physics |
|||
| title = Handbook of Teichmüller theory, Vol. VI |
|||
| volume = 27 |
|||
| year = 2016}} |
|||
* {{citation |
|||
| last = van Schooten | first = Frans | author-link = Frans van Schooten |
|||
| pages = 49–50, 69–70 |
|||
| title = De Organica Conicarum Sectionum In Plano Descriptione, Tractatus. Geometris, Opticis; Præsertim verò Gnomonicis et Mechanicis Utilis. Cui subnexa est Appendix, de Cubicarum Æquationum resolutione |
|||
| url = https://echo.mpiwg-berlin.mpg.de/ECHOdocuView?url=/mpiwg/online/permanent/library/EWN480XH/pageimg&start=61&viewMode=images&mode=imagepath&pn=69 |
|||
| year = 1646}} |
|||
* {{citation |
|||
| last = Yates | first = Robert C. |
|||
| date = March 1941 |
|||
| doi = 10.2307/3028413 |
|||
| issue = 6 |
|||
| journal = National Mathematics Magazine |
|||
| jstor = 3028413 |
|||
| pages = 278–293 |
|||
| title = The trisection problem |
|||
| volume = 15}} |
|||
{{refend}} |
|||
== Спољашње везе == |
== Спољашње везе == |
||
Верзија на датум 25. јун 2023. у 08:33
| Четвороугао | |
|---|---|
 Различити типови четвороугла | |
| Ивице и темена | 4 |
| Симбол Шлефли | {4} (за квадрат) |
| Површина | разни методи |
| Унутрашњи угао (степени) | 90° (за квадрат и правоугаоник) |
Четвороугао је у геометрији у равни затворени геометријски облик кога окружују четири дужи спојене у четири темена.[1] Формална дефиниција четвороугла каже да је четвороугао многоугао који има четири темена. Сваки четвороугао има тачно две дијагонале. Дијагонала је дуж која спаја два несуседна темена. Други назив за општи четвороугао је трапезоид. Трапезоиди (као нпр. делтоид) немају паралелне странице.
Реч „квадрилатералан” је изведена из латинских речи quadri, варијанте речи четири, и latus, са значењем „страна”. Квадрилатерали су једноставни (без самопресецања) или комплексни (самопресецајући), који се такође називају укрштеним. Једноставни четвороугли су или конвексни или конкавни. Четвороугао са врховима , , и се понекад означава као .[2]
Унутрашњи углови једноставног (и планарног) четвороугла ABCD имају суму од 360 угаоних степени,[2] односно Ово је посебан случај формуле суме унутрашњих углова (n − 2) × 180°.[3] Сви четвороугаоници без самоукрштања постављају раван формирану поновљеном ротацијом око средишта њихових ивица.[4]
Подела четвороуглова
Четвороуглови се пре свега деле на конвексне и неконвексне. Неконвексни се деле на четвороуглове са и без самопресека. Потребан и довољан услов да четвороугао буде конвексан је да се дијагонале четвороугла секу.[5][6]
Основна подела конвексних четвороуглова је према броју парова паралелних страница. Приметимо да суседне странице многоугла не могу бити паралелне, јер се праве које их садрже секу у темену многоугла. Сваке две странице троугла су суседне, па наведена подела није била применљива на троуглове. Конвексан четвороугао који има један пар паралелних страница зовемо трапез,[7][8] а онај који има два пара паралелних страница зовемо паралелограм.
Напомена. У литератури постоји извесно неслагање по питању тога да ли је скуп паралелограма подскуп скупа трапеза или су то два дисјунктна скупа. Ствар је у различитим интерпретацијама дефиниције трапеза. Док једни сматрају да је трапез сваки четвороугао који има бар један пар паралелних страница, други преферирају да трапезом називају само онај четвороугао који има тачно један пар паралелних страница.
У сврху сажетости даљег излагања наводимо дефиниције основице и крака трапеза. Паралелне странице трапеза зовемо основице, а преостале две странице краци. Ако крак посматрамо као трансверзалу, онда видимо да су два угла која належу на крак суплементни, као углови са паралелним крацима.
Појмови тангентан многоугао и тетиван многоугао применљиви су и у случају четвороугла.
Конвексни четвороуглови се деле на тангентне (оне у које се може уписати круг) и тетивне (оне око којих се може описати круг) четвороуглове и на општи случај трапеза, четвороугла коме су две наспрамне странице паралелне. Четвороуглови који су истовремено тетивни и тангентни се још зову и бицентричним.
Специјалан случај тангентног четвороугла је делтоид, који има два пара суседних међусобно једнаких страница.
Општи трапез има још три специјална подслучаја:
- Паралелограм или ромбоид,
- Правоугли трапез, коме је бар један (па онда и њему суплементан) угао прав,[9]
- Једнакокраки трапез, који има једнаке углове на основици или једнаке дијагонале, а тиме и једнаке краке. Овај трапез је такође тетивни четвороугао.
Напомена. Иако је наведена дефиниција на први поглед у нескладу са називом једнакокраког трапеза, њоме се избегава сложеност у навођењу особина једнакокраког трапеза и његовог места у подели четвороуглова. Наиме, ако би једнакокраки трапез био дефинисан као трапез чији су краци једнаки, онда би обухватио паралелограм, а изгубио би све друге наведене особине (тетивност, једнакост дијагонала, углова на основици).
Паралелограм има два специјална случаја:
- Ромб је четвороугао коме су све странице једнаке, а специјалан је случај паралелограма и делтоида,[10]
- Правоугаоник је четвороугао коме су сви углови (или бар три) прави и такође је специјалан случај паралелограма. Ако прихватамо дефиницију трапеза која обухвата паралелограме, онда је правоугаоник осим тога специјалан случај и једнакокраког и правоуглог трапеза.
Квадрат је специјалан случај паралелограма који има особине ромба и правоугаоника: сви углови су му прави и све странице су му међусобно једнаке. Квадрат је пример бицентричног четвороугла. Квадрат се може дефинисати као правилан четвороугао. Квадрат је такође и специјалан случај делтоида јер има три права угла.
Формуле
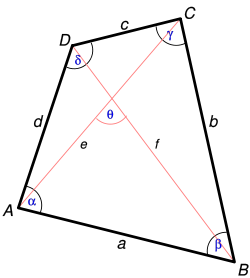
Збир углова у четвороуглу је једнак 360° односно 2π:
Ако је угао Θ прав, наспрамне странице се могу посматрати као катете правоуглих троуглова који имају исту дужину хипотенузе:
Површина четвороугла може бити изражена на следеће начине:
- ,
- ,
- .
Референце
- ^ Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] изд.). New York: Dover Publications. In 3 vols.: vol. 1 ISBN 0-486-60088-2, vol. 2 ISBN 0-486-60089-0, vol. 3 ISBN 0-486-60090-4
- ^ а б „Quadrilaterals - Square, Rectangle, Rhombus, Trapezoid, Parallelogram”. Mathsisfun.com. Приступљено 2020-09-02.
- ^ „Sum of Angles in a Polygon”. Cuemath. Приступљено 22. 6. 2022.
- ^ Martin, George Edward (1982), Transformation geometry, Undergraduate Texts in Mathematics, Springer-Verlag, Theorem 12.1, page 120, ISBN 0-387-90636-3, MR 718119, doi:10.1007/978-1-4612-5680-9
- ^ James A. H. Murray (1926). A New English Dictionary on Historical Principles: Founded Mainly on the Materials Collected by the Philological Society. X. Clarendon Press at Oxford. стр. 286 (Trapezium). „With Euclid (c 300 B.C.) τραπέζιον included all quadrilateral figures except the square, rectangle, rhombus, and rhomboid; into the varieties of trapezia he did not enter. But Proclus, who wrote Commentaries on the First Book of Euclid's Elements A.D. 450, retained the name τραπέζιον only for quadrilaterals having two sides parallel, subdividing these into the τραπέζιον ἰσοσκελὲς, isosceles trapezium, having the two non-parallel sides (and the angles at their bases) equal, and σκαληνὸν τραπέζιον, scalene trapezium, in which these sides and angles are unequal. For quadrilaterals having no sides parallel, Proclus introduced the name τραπέζοειδὲς TRAPEZOID. This nomenclature is retained in all the continental languages, and was universal in England till late in the 18th century, when the application of the terms was transposed, so that the figure which Proclus and modern geometers of other nations call specifically a trapezium (F. trapèze, Ger. trapez, Du. trapezium, It. trapezio) became with most English writers a trapezoid, and the trapezoid of Proclus and other nations a trapezium. This changed sense of trapezoid is given in Hutton's Mathematical Dictionary, 1795, as ‘sometimes’ used -- he does not say by whom; but he himself unfortunately adopted and used it, and his Dictionary was doubtless the chief agent in its diffusion. Some geometers however continued to use the terms in their original senses, and since c 1875 this is the prevalent use.”
- ^ Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (5. 4. 2016). The Symmetries of Things. CRC Press. стр. 286. ISBN 978-1-4398-6489-0.
- ^ http://www.mathopenref.com/trapezoid.html Mathopenref definition
- ^ A. D. Gardiner & C. J. Bradley, Plane Euclidean Geometry: Theory and Problems, UKMT, 2005, p. 34.
- ^ „Types of Quadrilaterals”. Basic-mathematics.com.
- ^ „CIMT - Page no longer available at Plymouth University servers” (PDF). www.cimt.plymouth.ac.uk. Архивирано из оригинала (PDF) 2014-05-14. г.
Литература
- Abbott, Timothy Good (2008), „3.1.2 Contraparallelograms”, Generalizations of Kempe's Universality Theorem (PDF) (Master's thesis), Massachusetts Institute of Technology, стр. 34—36
- Coxeter, H. S. M.; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), „Uniform polyhedra”, Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 246 (916): 401—450, Bibcode:1954RSPTA.246..401C, JSTOR 91532, MR 0062446, S2CID 202575183, doi:10.1098/rsta.1954.0003
- Alsina, Claudi; Nelsen, Roger B. (2020), A Cornucopia of Quadrilaterals, The Dolciani Mathematical Expositions, 55, Providence, Rhode Island: MAA Press and American Mathematical Society, стр. 212, ISBN 978-1-4704-5312-1, MR 4286138
- Cundy, H. Martyn (март 2005), „89.23 The lemniscate of Bernoulli”, The Mathematical Gazette, 89 (514): 89—93, S2CID 125521872, doi:10.1017/s0025557200176855
- Begalla, Engjëll; Perucca, Antonella (2020), „The ABCD of cyclic quadrilaterals”, Uitwiskeling, University of Luxembourg, hdl:10993/43232
- Dijksman, E. A. (1976), Motion Geometry of Mechanisms, Cambridge University Press, стр. 203, ISBN 9780521208413
- Demaine, Erik; O'Rourke, Joseph (2007), Geometric Folding Algorithms, Cambridge University Press, стр. 32—33, ISBN 978-0-521-85757-4, MR 2354878, doi:10.1017/CBO9780511735172
- Grebenikov, Evgenii A.; Ikhsanov, Ersain V.; Prokopenya, Alexander N. (2006), „Numeric-symbolic computations in the study of central configurations in the planar Newtonian four-body problem”, Computer algebra in scientific computing, Lecture Notes in Comput. Sci., 4194, Berlin: Springer, стр. 192—204, MR 2279793, doi:10.1007/11870814_16
- Glaeser, Georg (2020), „Antiparallelograms; It does not always have to be a uniform rotation ...”, Geometry and its Applications in Arts, Nature and Technology, Springer International Publishing, стр. 428—429, ISBN 978-3-030-61397-6, doi:10.1007/978-3-030-61398-3
- De Villiers, Michael (2015), „Slaying a geometrical 'monster': finding the area of a crossed quadrilateral”, Learning and Teaching Mathematics, 2015 (18): 23—28, hdl:10520/EJC175721
- Muirhead, R. F. (фебруар 1901), „Geometry of the isosceles trapezium and the contra-parallelogram, with applications to the geometry of the ellipse”, Proceedings of the Edinburgh Mathematical Society, 20: 70—72, doi:10.1017/s0013091500032892

- Norton, Robert L. (2003), Design of Machinery, McGraw-Hill Professional, стр. 51, ISBN 978-0-07-121496-4
- Bryant, John; Sangwin, Christopher J. (2008), „3.3 The Crossed Parallelogram”, How Round Is Your Circle? Where Engineering and Mathematics Meet, Princeton University Press, стр. 54—56, ISBN 978-0-691-13118-4
- Sossinsky, Alexey (2016), „Configuration spaces of planar linkages”, Handbook of Teichmüller theory, Vol. VI, IRMA Lectures in Mathematics and Theoretical Physics, 27, Zürich: European Mathematical Society, стр. 335—373, MR 3618193
- van Schooten, Frans (1646), De Organica Conicarum Sectionum In Plano Descriptione, Tractatus. Geometris, Opticis; Præsertim verò Gnomonicis et Mechanicis Utilis. Cui subnexa est Appendix, de Cubicarum Æquationum resolutione, стр. 49—50, 69—70
- Yates, Robert C. (март 1941), „The trisection problem”, National Mathematics Magazine, 15 (6): 278—293, JSTOR 3028413, doi:10.2307/3028413
Спољашње везе
- Четвороугао на mathworld.wolfram.com (језик: енглески)
- Дефиниција и особине четвороугла, са интерактивном анимацијом (језик: енглески)
- Примери конструкција четвороугла
- Hazewinkel Michiel, ур. (2001). „Quadrangle, complete”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104.
- Weisstein, Eric W. „Quadrilateral”. MathWorld.
- Encyclopedia of Quadri-Figures by Chris Van Tienhoven
- Compendium Geometry Analytic Geometry of Quadrilaterals
- Quadrilaterals Formed by Perpendicular Bisectors, Projective Collinearity and Interactive Classification of Quadrilaterals from cut-the-knot
- Definitions and examples of quadrilaterals and Definition and properties of tetragons from Mathopenref
- A (dynamic) Hierarchical Quadrilateral Tree at Dynamic Geometry Sketches
- An extended classification of quadrilaterals Архивирано на сајту Wayback Machine (30. децембар 2019) at Dynamic Math Learning Homepage Архивирано на сајту Wayback Machine (25. август 2018)
- Quadrilateral Venn Diagram Quadrilaterals expressed in the form of a Venn diagram, where the areas are also the shape of the quadrilateral they describe.
- The role and function of a hierarchical classification of quadrilaterals by Michael de Villiers











