Orbita

Kao pojam u fizici, orbita je put koje jedno telo čini oko drugog tela dok je pod uticajem neke sile.^[1] Orbite je prvi izučavao Johan Kepler koji je otkrio Keplerove zakone o kretanju planeta (v. Drugi Keplerov zakon). Orbite mogu biti kružne, parabolične, eliptične, hiperbolične, a planete kruže oko Sunca po elipsi (vidi ekscentricitet). Svaka orbita je određena sa orbitalnim elementima koji tačno opisuju orbitu, kao i položaj tela na njoj. Orbitalnih elemenata ima šest i oni su: ekscentricitet, velika poluosa, inklinacija, longituda uzlaznog čvora, argument perihela i prava anomalija.

Baricentar, težište ili centar masa je tačka oko koje se kreću tela dvojnog ili višestrukog sistema. Na slici je sličan sistem kao Sunce - Zemlja.

Orbita kretanja planeta oko Sunca je elipsa

Baricentar sistema Zemlje i Meseca nalazi se unutar Zemljine površine na udaljenosti 4 670 km od središta. Ta se tačka sistema, a ne središte Zemlje, kreće po eliptičnoj stazi oko Sunca.

Dva nebeska tela različitih masa okreću se oko zajedničkog baricentra (centra masa). Na slici je sličan sistem kao Pluton - Haron.

Sa smanjenjem ekscentriciteta (ε → 0) elipsa prelazi u kružnicu, a njena velika poluosa prelazi u poluprečnik kružnice. Ulogu srednje udaljenosti ima tada sam poluprečnik kružnice. S druge strane, s povećanjem ekscentriciteta (ε → 1) elipsa prelazi u parabolu. Za hiperbolu vredi ε > 1.

Plutonova putanja u ravni ekliptike. Ravni putanja Neptuna i Plutona seku pod uglom od oko 15°.

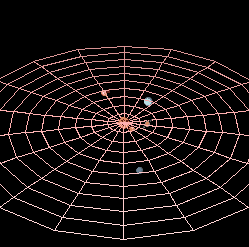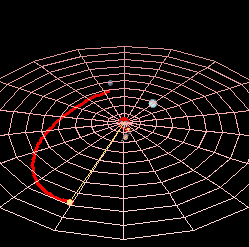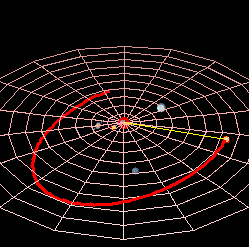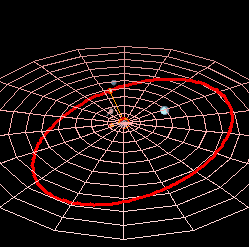
Planetarna putanja u astronomiji i astronautici, je putanja u obliku konike po kojoj se kreće nebesko telo manje mase u gravitacionom polju nebeskog tela veće mase. Zatvorena orbita nebeskih tela elipsa je sa žarištem u kojem se nalazi središnje fizičko telo ili središte mase. Takve su orbite planeta i njihovih prirodnih satelita u Sunčevom sistemu. Zatvorena orbita nebeskih tela elipsa je sa žarištem u kojem se nalazi središnje fizičko telo ili središte mase. Takve su orbite planeta i njihovih prirodnih satelita u Sunčevom sistemu. Otvorena orbita je parabola (na primer orbita nekih kometa) ili hiperbola.

Orbite veštačkih satelita, koje mogu biti kružne ili eliptične, označavaju se s obzirom na način kretanja oko Zemlje:

geosinhrona orbita ima period 1 dan, dok je geostacionarna orbita ona geosinhrona orbita kojom se satelit postavlja iznad istog položaja na Zemljinoj površini;
polarna orbita, odnosno kvazipolarna orbita, prelazi preko polova, odnosno blizu njih;
sa Suncem sinhronizovana orbita ima ravan uvek uperenu u Sunce ili pod stalnim ugaonim odmakom od Sunca, a satelit prelazi preko ekvatora uvek u isto doba dana;
prelazna orbita, uvedena radi ekonomičnosti, orbita je između početne i konačne orbite pri postavljanju veštačkih satelita.
orbita za parkiranje privremena je orbita veštačkog satelita;
prolećna orbita je orbita kojom svemirska letelica prolazi pokraj nebeskog tela (na primer Meseca ili neke planete).^[2]

Johan Kepler je prvi pronašao svoje zakone planetarnog kretanja. Otkrio je da su putanje planeta u našem Sunčevom sistemu eliptične.

Prvi Keplerov zakon i planetarne putanje

Prvi Keplerov zakon utvrđuje geometrijske osobine planetarnih putanja. J. Kepler je našao da su staze elipse, a da se Sunce nalazi u jednom od žarišta.^[3] Kako je Sunce zajedničko svim planetama, tako je Sunce u žarištu koje je zajedničko svim eliptičnim stazama. To je jedini uslov i nema daljih ograničenja, te položaj putanje u prostoru može biti veoma raznolik. Na skicama koje prikazuju dve ili više planetarnih putanja, one se nalaze u istoj ravni. Generalno, velike poluose dve elipse se ne podudaraju ni po smeru, ni po veličini, ni po ravnima u kojima se nalaze.

Veličina i izduženost elipse određena je velikom poluosom a i ekscentricitetom e. Velika poluosa a ujedno je i srednja udaljenost tačke na elipsi od jednog žarišta (planeta od Sunca). Kada je telo najdalje od Sunca u afelu, njegova je provodnica (radijusvektor) najveća i iznosi:

\,r_{\max }=a+e

Kada je planeta najbliža Suncu (kada je u perihelu), tada joj je provodnica najmanja i iznosi:

\,r_{\min }=a-e

Aritmetička sredina najveće i najmanje udaljenosti planete od Sunca ili srednja udaljenost jednaka je velikoj poluosi a:

a={\frac {r_{\mathrm {max} }+r_{\mathrm {min} }}{2}}.

Izduženost putanje iskazuje se numeričkim ekscentricitetom ε koji je jednak odnosu linearnog ekscentriciteta i velike poluose staze:

\varepsilon ={\frac {e}{a}}={\frac {\sqrt {a^{2}-b^{2}}}{a}}

ε je bezdimenzionalna veličina. Sa smanjenjem ekscentriciteta (ε → 0) elipsa prelazi u kružnicu, a njena velika poluosa prelazi u poluprečnik kružnice. Ulogu srednje udaljenosti ima tada, naravno, sam poluprečnik kružnice. S druge strane, s povećanjem ekscentriciteta (ε → 1) elipsa prelazi u parabolu. Za hiperbolu vredi ε > 1. Parabola i hiperbola nisu zatvorene krive.

Veličine planetarnih putanja

Položaj planetarne putanje u prostoru treba odrediti pomoću poznatih orijentira. Zato se upotrebljava ravan ekliptike i prolećna tačka. Ugao između ravni u kojoj se nalazi staza tela i ravni ekliptike zove se nagib ili inklinacija (oznaka: i). Dve se ravni seku u pravcu na kojemu su dve tačke istaknute - one u kojima planetarna putanja probada ravan ekliptike: uzlazni čvor Ω (u njemu telo u svom godišnjem kretanju prelazi sa južne strane ekliptike na severnu) i silazni čvor Ʊ (u njemu telo u svom godišnjem kretanju prelazi sa severne strane ekliptike na južnu). Položaj uzlaznog čvora zadaje se ekliptičkom dužinom uzlaznog čvora Ω. S merama i i Ω orijentisana je ravan kretanja nebeskog tela u prostoru. Da bi se u toj ravni orijentisala elipsa, belježi se položaj njenog perihela. U tu svrhu služi argument perihela π, ugao od uzlaznog čvora do velike poluose koja sadrži perihel. Longitudom perihela naziva se ukupan ugao ω = Ω + π.

Da bi se pratilo kretanje nebeskog tela, potrebno je dodati podatak o zvezdanom (sideričkom) ophodnom vremenu P i o trenutku t_o u kojem telo prolazi perihelom. Dakle, za opis geometrijskih svojstava planetarnih putanja - veličine elipse, oblika elipse, njene orijentacije i načina kretanja tela - potrebno je 7 veličina: a, e, i, Ω, ω, P i t_o. To su veličine planetarnih putanja.

Analiza planetarnih putanja

Većina planeta ima slabo izdužene planetarne putanje (staze), koje je na malom crtežu okom teško razlikovati od kružnice. Tako Zemljina putanja s ε = 0,001673 ima veliku poluosu a = 149,597 ∙ 10⁶ km, malu poluosu b = 149,577 ∙ 10⁶ km, najmanju udaljenost od Sunca r_min = 147,1 ∙ 10⁶ km i najveću udaljenost od Sunca r_max = 152.1 ∙ 10⁶ km.

Staze planetoida u proseku su jače izdužene os planetnih putanja. Kod kometa je šarolikost mnogo veća. Neke komete imaju numerički ekscentricitet ε blizak jedinici.

Najizduženiju stazu ima Merkur (e = 0,205), dok najmanji ekscentricitet ima Venera (e = 0,007).

Razlike se opažaju i u nagibima planetarnih putanja. Plutonova i Merkurova staza najviše se od svih planeta otklanjaju od Zemljine putanje. Kod Plutona to dovodi do zanimljive posledice. Naime, crtaju li se staze Neptuna i Plutona projektovane u istu ravninu, čini se da se zbog izduženosti Plutonove staze te dve putanje seku, te da se dve planete mogu i sudariti. Neptun je zaista u nekim razdobljima dalje od Sunca nego Pluton (na primer kao od 1980. do 1999). Međutim kako se ravni putanja Neptuna i Plutona seku pod uglom od oko 15°, te su staze uvek daleko jedna od druge. Stoga se oni nikada ne mogu sudariti.

Putanje planetoida nagnute su prema ekliptici za više desetina stupnjeva, ravni kometa mogu seći ekliptiku pod bilo kojim uglom. Kada je ugao inklinacije veći od 180°, kaže se da je putanja nebeskog tela i njegova revolucija retrogradna; projektujući takvu stazu na ravan ekliptike, videlo bi se da se telo kreće oko Sunca u suprotnom smislu od Zemlje i ostalih planeta. Sve planete i planetoidi imaju direktnu revoluciju. Fizički različite vrste tela u Sunčevom sistemu se grupišu po geometrijskim svojstvima putanja. Do razlika u vladanju nebeskih tela došlo je u toku razvoja Sunčevog sistema.

Generalno, veličine planetarnih putanja pojedinog člana Sunčevog sistema neprestano se menjaju. Promena tih veličina kod Zemlje mogla je u prošlosti, u dugim geološkim razdobljima, uticati na klimatske promene.

Može se zapaziti još da se velika poluosa (linija koja povezuje najbliži i najudaljeniji položaj tela od Sunca, perihel i afel), nazvana još i linija apsida, ne podudara s linijom koja povezuje zimsku i letnju tačku. Razlika se u stvari stalno povećava, jer se linija apsida zakreće u liniji putanje; zakreće se u smeru kretanja Zemlje, te Zemlji treba više vremena da ponovo stigne u perihel, nego što joj treba da ponovi svoj položaj prema zvezdama. Drugim rečima, zvezdana (siderička) godina kraća je od vremena prolaska Zemlje perihelom. To razdoblje traje 365 d 6 h 13 min 53 s = 365,25964 dan i zove se anomalistička godina (godina).^[4]

Zemljina putanja

Zemljina putanja u astronomiji prestavlja planetarnu putanju (orbitu) Zemlje kojom obilazi Sunce, na udaljenosti od jedne astronomske jedinice (AJ) ili 149 597 870 691 ± 30 metara, što prestavlja približno 150 miliona kilometara.^[5]^[6] Perihel Zemlje je najbliža tačka Zemljine putanje do Sunčevog središta, smeštena na kraju velike ose elipse kojom se Zemlja kreće relativno prema Suncu, a Zemlja prolazi kroz perihel svake godine početkom januara (u zadnje vreme 3. januara) i iznosi 147 098 291 km. Afel Zemlje je najudaljenija tačka putanje Zemlje do Sunčevog središta, a Zemlja prolazi kroz afel početkom jula (u zadnje vreme 4. jula) i iznosi 152 098 233 km. Orbitalna brzina Zemlje je 30 km/s (108 000 km/h) što znači da pređe udaljenost Zemljinog prečnika (oko 12 700 km) za 7 minuta ili udaljenost do Meseca (oko 384 000 km) za 4 sata.

Референце

^ Fitzpatrick, Richard (2. 2. 2006). „Planetary orbits”. Classical Mechanics – an introductory course. The University of Texas at Austin. Архивирано из оригинала 3. 3. 2001. г.
^ orbita, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2018.
^ Wilson, Curtis (мај 1994). „Kepler's Laws, So-Called” (PDF). HAD News (31): 1—2. Приступљено 27. 12. 2016.
^ Vladis Vujnović : "Astronomija", Školska knjiga, 1989.
^ „Sun: Facts & Figures”. Solar System Exploration. National Aeronautics and Space Administration. Архивирано из оригинала 3. 7. 2015. г. Приступљено 29. 7. 2015.
^ Jean Meeus, Astronomical Algorithms 2nd ed, ISBN 0-943396-61-1 (Richmond, VA: Willmann-Bell, 1998) 238. See Ellipse#Circumference. The formula by Ramanujan is accurate enough.

Literatura

Abell; Morrison; Wolff (1987). Exploration of the Universe (fifth izd.). Saunders College Publishing.
Linton, Christopher (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy. Cambridge University Press. ISBN 978-1-139-45379-0.
Frank Swetz; John Fauvel; Bengt Johansson; Victor Katz; Otto Bekken (1995). Learn from the Masters. MAA. ISBN 978-0-88385-703-8.
Andrea Milani and Giovanni F. Gronchi. Theory of Orbit Determination (Cambridge University Press; 378 pages; 2010). Discusses new algorithms for determining the orbits of both natural and artificial celestial bodies.
Roger, R. Bate; Mueller, Donald D.; White, Jerry E. (1971). Fundamentals of Astrodynamics. Dover Books on Astronomy and Astrophysics. New York: Dover Publications. str. 21. ISBN 0486600610. LCCN 73157430.
El'Yasberg "Theory of flight of artificial earth satellites", Israel program for Scientific Translations (1967)
Bate, Roger; Mueller, Donald; White, Jerry (1971). Fundamentals of Astrodynamics. Dover Publications, Inc., New York. ISBN 0-486-60061-0.
Copernicus, Nicolaus (1952), „Book I, Chapter 4, The Movement of the Celestial Bodies Is Regular, Circular, and Everlasting-Or Else Compounded of Circular Movements”, On the Revolutions of the Heavenly Spheres, Great Books of the Western World, 16, Prevod: Charles Glenn Wallis, Chicago: William Benton, str. 497—838

Spoljašnje veze

CalcTool: Orbital period of a planet calculator. Has wide choice of units. Requires JavaScript.
Java simulation on orbital motion. Requires Java.
NOAA page on Climate Forcing Data includes (calculated) data on Earth orbit variations over the last 50 million years and for the coming 20 million years
On-line orbit plotter. Requires JavaScript.
Orbital Mechanics (Rocket and Space Technology)
Orbital simulations by Varadi, Ghil and Runnegar (2003) provide another, slightly different series for Earth orbit eccentricity, and also a series for orbital inclination. Orbits for the other planets were also calculated, by F. Varadi; B. Runnegar; M. Ghil (2003). „Successive Refinements in Long-Term Integrations of Planetary Orbits”. The Astrophysical Journal. 592 (1): 620—630. Bibcode:2003ApJ...592..620V. doi:10.1086/375560 . , but only the eccentricity data for Earth and Mercury are available online.
Understand orbits using direct manipulation Arhivirano na sajtu Wayback Machine (8. novembar 2017). Requires JavaScript and Macromedia
Merrifield, Michael. „Orbits (including the first manned orbit)”. Sixty Symbols. Brady Haran for the University of Nottingham.
Planetary orbit Simulator Astronoo

[1] Fitzpatrick, Richard (2. 2. 2006). „Planetary orbits”. Classical Mechanics – an introductory course. The University of Texas at Austin. Архивирано из оригинала 3. 3. 2001. г.

[2] orbita, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2018.

[Wilson_1994-3] Wilson, Curtis (мај 1994). „Kepler's Laws, So-Called” (PDF). HAD News (31): 1—2. Приступљено 27. 12. 2016.

[4] Vladis Vujnović : "Astronomija", Školska knjiga, 1989.

[5] „Sun: Facts & Figures”. Solar System Exploration. National Aeronautics and Space Administration. Архивирано из оригинала 3. 7. 2015. г. Приступљено 29. 7. 2015.

[AA-6] Jean Meeus, Astronomical Algorithms 2nd ed, ISBN 0-943396-61-1 (Richmond, VA: Willmann-Bell, 1998) 238. See Ellipse#Circumference. The formula by Ramanujan is accurate enough.

[1]

[2]

[3]

[4]

[5]

[6]

Normativna kontrola
Državne	Nemačka Izrael Sjedinjene Države Letonija
Ostale	Enciklopedija Britanika 2