Златни пресек

${\frac {a+b}{a}}={\frac {a}{b}}$

Златни правоугаоник (у ружичастом) са дужом страном a и краћом страном side b, када је постављен поред квадрата дужине a, произвешће геометријску сличност златног правоугаоника са дужом страном a + b и краћом страном a. Ово илуструје однос ${\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi$.

У математици две величине су у златном односу, ако је однос између две величине једнак односу суме те две вредности наспрам веће вредности. Слика на десној страни илуструје геометријски однос. Алгебарски, за количине a и b и a > b > 0,

${\frac {a+b}{a}}={\frac {a}{b}}\ {\stackrel {\text{def}}{=}}\ \varphi ,$

грчко слово фи ($\varphi$ или $\phi$) представља константу. Њена вредност је:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.6180339887\ldots .$  A001622

Златни однос има и назив златни пресек (латински: sectio aurea).. Остали називи укључују крајња и средња размера, екстремни однос, средишњи пресек, златна пропорција, и златни број. Sectio divina лат. (изговор: секцио дивина). Божанствени пресјек. Овај однос дужи примјењен на предметима, сликама итд. изазива посебан естетски доживљај – допадање, па отуда и назив „Божански пресјек“.

Златни однос се појављује у неким шаблонима у природи, укључујући phyllotaxis (спирално ређање листова) и у другим деловима биљака.

Математичари још од Еуклида су проучавали својства златног односа, укључујући појављивање у димензијама правилног петоугла и у златном правоугаонику, који може да се подели у квадрат и још један правоугаоник истог односа.

Историја

Теорија златног пресека започета је у антици, а свој процват имала је у ренесанси када су уметници, математичари, физичари и астролози тражили савршенство у композицијама познатих структура.

Херодот (484. - 424. п. н. е.) је записао: „Један египатски свештеник говорећи о облику Кеопсове пирамиде споменуо ми је да је квадрат над њеном висином једнак површини бочног троугла.”

Математичка пирамида

$v={\frac {a}{2}}{\sqrt {\varphi }}$

$b={\frac {a}{2}}{\sqrt {\varphi +2}}$

$\alpha =\operatorname {arctg} {\sqrt {\varphi }}$

$\beta =\operatorname {arctg} {\sqrt {\frac {\varphi }{2}}}$

Грчки кипар Фидије у V веку п. н. е. применио је златни пресек у дизајну својих скулптура и градњи Партенона. Платон (грчки филозоф, V i IV век пне) у „Тимотеју” описује пет правилних геометријских тела као основу хармоничне структуре света. Златни пресек игра кључну улогу у димензијама и обликовању неких од ових тела. Питагорејци (око 500. године п. н. е.) долазе до једног од најважнијих открића у математици: дијагонала и страница квадрата (правилног петоугла) су несамерљиве.

Златни троугао унутар златног троугла

${\frac {d}{a_{5}}}=\varphi$

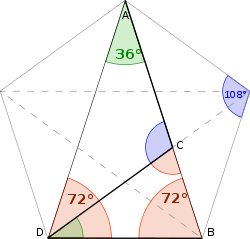
Грчки математичар Еуклид први је овај број уочио и математички изразио. Око 300 година п. н. е. написао је књигу „Елементи” у којој наводи прву забележену дефиницију златног пресека.

Дата дужина се може поделити тако да правоугаоник обухваћен целом дужином и једним одсечком, буде једнак квадрату на другом одсечку.

$a(a-x)=x^{2}$

$x^{2}+ax-a^{2}=0$

$x={\frac {-1+{\sqrt {5}}}{2}}a$

Сва знања старих Грка објединио је римски архитекта Марко Витрувије у делу De architectura libri decem или Десет књига о архитектури, посвећеном императору Августу. Писао је о симетрији храмова, а њихове пропорције упоређује с размерама човечијег тела. Витрувије је уцртао људско тело у кружницу, што је касније поново интерпретирао Леонардо Да Винчи. Лука Пачоли (1446–1510) штампао је у Венецији 1509. дело De divina proportione, које је имало велики утицај и након којег златни пресек доживљава праву ренесансу. У њему описује хармонијске особине „божанске размере”. Књигу је илустровао Леонардо да Винчи.

Мартин Ом је 1835. године у другом издању уџбеника Die reine Elementar - Mathematik (Чиста елементарна математика) први пут користи термин златни пресек. Ознаку $\varphi$ је 1909. предложио амерички математичар Марк Бар у част славног старогрчког кипара Фидије (480–430. п. н. е.)

Прорачун

Бинарни	1.1001111000110111011...
Декадни	1.6180339887498948482...  A001622
Хексадецимални	1.9E3779B97F4A7C15F39...
Верижни разломак	$1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}$
Алгебарски облик	${\frac {1+{\sqrt {5}}}{2}}$
Бесконачни ред	${\frac {13}{8}}+\sum _{n=0}^{\infty }{\frac {(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}}$

Две величине a и b су у златном односу φ ако

${\frac {a+b}{a}}={\frac {a}{b}}=\varphi .$

Један метод за проналажење вредности φ је са решавањем леве стране. Упрошћавањем разломка и заменом у b/a = 1/φ,

${\frac {a+b}{a}}=1+{\frac {b}{a}}=1+{\frac {1}{\varphi }}.$

Стога је,

$1+{\frac {1}{\varphi }}=\varphi .$

Множењем са φ даје

$\varphi +1=\varphi ^{2}$

које може да се изрази као

${\varphi }^{2}-\varphi -1=0.$

Коришћењем формуле за решавање квадратне једначине, добијају се два решења:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\dots$

и

$\varphi ={\frac {1-{\sqrt {5}}}{2}}=-0.6180\,339887\dots$

Зато што је φ однос између две позитивне вредности, φ је увек позитивна вредност:

$\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\dots$.

Алгебра

Ирационалност

Златни однос је ирационалан број. Испод су два кратка доказа o ирационалности:

Контрадикција изразу у најнижој вредности

Да је φ рационалан број, онда би био омер странама правоугаоника са целим странама (правоугаоник који обухвата цео дијаграм). Али би такође био и однос целобројних страна мањег правоугаоника (десни део дијаграма) добијен брисањем квадрата. Секвенца смањења целобројне вредности дужине странице формиране брисањем квадрата не може вечно трајати јер цели бројеви имају доње границе, стога φ не може бити рационалан.

Подсетимо се да:

целина је дужи део плус краћи део;

целина је дужи део као што је дужи део на краћи део.

Ако целину именујемо са n а дужи део са m, онда друга изјава постаје:

n је према m исто као што је m према n − m,

или, алгебарски

${\frac {n}{m}}={\frac {m}{n-m}}.\qquad (*)$

Тврдити да је φ рационалан значи да је φ однос n/m где су n и m цели бројеви. Можемо рећи и да n/m имају најниже вредности и да су n и m позитивни бројеви. Али ако је разломак n/m у најнижим вредностима, онда се идентитет обележава са (*) за горњу једначину m/(n − m) која и даље поседује најниже вредности. То је контрадикција која произлази из тврдње да је φ рационалан.

Извод из ирационалности броја √5

Још један кратак доказ — вероватно познатији — где ирационалност златног односа користи затвореност рационалних бројева код сабирања и множења. Ако је $\textstyle {\frac {1+{\sqrt {5}}}{2}}$ рационалан, онда је и $\textstyle 2\left({\frac {1+{\sqrt {5}}}{2}}\right)-1={\sqrt {5}}$ такође рационалан, што је противречно чињеници да је квадратни корен од не-квадрата природног броја ирационалан.

Најмањи полином

Златни однос је такође и алгебарски број а чак и алгебарски цео број (комплексан број који је корен унарног полинома). Најмањи полином гласи:

$x^{2}-x-1$

Због члана са степеном 2, овај полином у ствари има два корена, и друга вредност је сродник златном односу.

Сродник златног пресека

Друга корена вредност најмањег полинома x² - x - 1 је

$-{\frac {1}{\varphi }}=1-\varphi ={\frac {1-{\sqrt {5}}}{2}}=-0.61803\,39887\dots .$

Апсолутна вредност ове количине (≈ 0.618) одговара дужини односа у обрнутом смеру (дужина краће стране у односу на дужу страну, b/a), понекад позната под именом сродник златног пресека. Означава се великим словом фи ($\Phi$):

$\Phi ={1 \over \varphi }=\varphi ^{-1}=0.61803\,39887\ldots .$

Види још

• Златни правоугаоник

Литература

• Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 978-0-7679-0815-3. 
• Stakhov, Alexey P.; Olsen, Scott (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. Singapore: World Scientific Publishing. ISBN 978-981-277-582-5. 
• Doczi, György (2005) [1981]. The Power of Limits: Proportional Harmonies in Nature, Art, and Architecture. Boston: Shambhala Publications. ISBN 1-59030-259-1. 
• Huntley, H. E. (1970). The Divine Proportion: A Study in Mathematical Beauty. New York: Dover Publications. ISBN 0-486-22254-3. 
• Joseph, George G. (2000) [1991]. The Crest of the Peacock: The Non-European Roots of Mathematics (New изд.). Princeton, NJ: Princeton University Press. ISBN 0-691-00659-8. 
• Sahlqvist, Leif (2008). Cardinal Alignments and the Golden Section: Principles of Ancient Cosmography and Design (3rd Rev. изд.). Charleston, SC: BookSurge. ISBN 1-4196-2157-2. 
• Schneider, Michael S. (1994). A Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and Science. New York: HarperCollins. ISBN 0-06-016939-7. 
• Scimone, Aldo (1997). La Sezione Aurea. Storia culturale di un leitmotiv della Matematica. Palermo: Sigma Edizioni. ISBN 978-88-7231-025-0. 
• Walser, Hans (2001) [Der Goldene Schnitt 1993]. The Golden Section. Peter Hilton trans.. Washington, DC: The Mathematical Association of America. ISBN 0-88385-534-8. 
• Olsen, Scott (2006). The Golden Section: Nature's Greatest Secret. Glastonbury: Wooden Books. стр. 3. ISBN 978-1-904263-47-0. 
• Van Mersbergen, Audrey M (1998). „Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic”. Communication Quarterly. 46. "a 'Golden Rectangle' has a ratio of the length of its sides equal to 1:1.61803+. The Parthenon is of these dimensions.")
• Livio, Mario. „The Golden Ratio in Art: Drawing heavily from The Golden Ratio” (PDF). стр. 6. Архивирано из оригинала (PDF) 05. 11. 2019. г. Приступљено 11. 9. 2019. 
• Le Corbusier,, The Modulor, стр. 35 , as cited in Padovan, Richard, Proportion: Science, Philosophy, Architecture. 1999. стр. 320. ISBN 978-0-419-22780-9. . Taylor & Francis. : "Both the paintings and the architectural designs make use of the golden section".

Спољашње везе

• Hazewinkel Michiel, ур. (2001). „Golden ratio”. Encyclopaedia of Mathematics. Springer. ISBN 978-1556080104. 
• "Golden Section" by Michael Schreiber, Wolfram Demonstrations Project, 2007.
• Golden Section in Photography: Golden Ratio, Golden Triangles, Golden Spiral
• Weisstein, Eric W.. „Golden Ratio”. MathWorld. 
• „Researcher explains mystery of golden ratio”. PhysOrg. 21. 12. 2009. .
• Knott, Ron. „The Golden section ratio: Phi”.  Information and activities by a mathematics professor.
• „The Pentagram & The Golden Ratio”. Архивирано из оригинала 05. 11. 2007. г. Приступљено 20. 06. 2017. . Green, Thomas M. Updated June 2005. Archived November 2007. Geometry instruction with problems to solve.
• Schneider, Robert P. (2011). „A Golden Pair of Identities in the Theory of Numbers”. arXiv:1109.3216  [math.HO].  Proves formulas that involve the golden mean and the Euler totient and Möbius functions.
• „The Myth That Will Not Go Away”. Архивирано из оригинала 12. 11. 2020. г. Приступљено 28. 02. 2016. , by Keith Devlin, addressing multiple allegations about the use of the golden ratio in culture.