Јоханес Ридберг
| Јоханес Ридберг | |
|---|---|
 Јоханес Роберт Ридберг, шведски физичар | |
| Лични подаци | |
| Датум рођења | 8. новембар 1854. |
| Место рођења | Халмстад, Шведска-Норвешка |
| Датум смрти | 28. децембар 1919. (65 год.) |
| Место смрти | Лунд, Шведска |
| Образовање | Универзитет у Лунду |
| Научни рад | |
| Поље | Физика |
| Познат по | Ридберговој формули |
Јоханес Роберт Ридберг (швед. Johannes Rydberg; Халмстад, 8. новембар 1854 — Лунд, 28. децембар 1919) био је шведски физичар.[1] Јоханес Ридберг је у физици познат по Ридберговој формули која је 1888. године кориштена за предвиђање таласне дужине фотона емитоване променом у енергетским нивоима електрона у атому. Физичка константа познатија као Ридбергова константа преименована је након његове смрти Ридбергова јединица. Побуђени атоми са високим основним квантним бројем, представљен је као и у Ридберговој једначини, названи су Ридберговим атомима.[2] Један кратер на Месецу носи Ридбергово име. Јоханес је био активан на Лунд Универзитету у Шведској. Добио је докторат из математике 1879. године.[3] Од 1882. до 1919. године био је и професор на Лунд Универзитету. Још као студент је пронашао везу између линија на спектрографу и корисне масе атома водоника. Преминуо је 28. децембра 1919. године.[4][5]
Јоханес се бавио проучавањем оптичких спектара. Први је уочио да се таласни бројеви атомских спектара свих хемијских елемената могу приказати као умножак два фактора, од којих је један промењив (варијабилан), а други сталан (константан). Тај константни фактор добио је назив Ридбергова константа. Борова је теорија, међутим, показала, а после су тачнија мерења то и потврдила, да се Ридбергова константа понешто разликује од хемијског елемента и да је њена права вредност Р за дати елемент:
где је: m - маса електрона, M+ - маса једноструко јонизованог атома дотичног елемента, а R∞ - универзална Ридбергова константа, то јест:
где је: e - електрични набој електрона, c - брзина светлости, h - Планкова константа.
Био је члан Краљевског друштва (енгл. Royal Society) од 1919. По њем су названи кратер на Месецу (Ридберг (кратер)) и планетоид (10506 Ридберг).[6] Побуђени атоми, с врло високим квантним бројевима, а које преставља број n у Ридберговој формули, називају се Ридбергови атоми. Ридбергова предвиђања да ће водоникове спектралне линије, која се добију из Ридбергове формуле, помоћи у теоретском разумевању атомске структуре, искористио је 1913. Н. Бор и створио Боров модел атома. У спектроскопији се користи константа, која се заснива на теоретском атому бесконачне масе, и назива се Ридберг (R) у његову част.
Искуствене чињенице о спектрима[уреди | уреди извор]




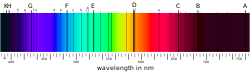
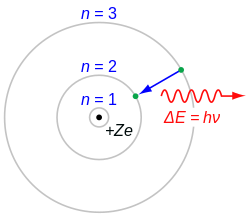




Ужарена чврста тела емитују светлост с континуирано расподељеним таласним дужинама (топлотно зрачење). Од температуре ужареног тела зависи који је део спектра најјачи (најинтензивнији), али од места максимума постепено се гаси светлост према мањим и већим таласним дужинама. Насупрот томе континуираном спектру чврстих тела опажа се код плинова и пара нешто друго. У њиховом се спектру појављују дискретне линије, које су својствене за поједине хемијске елементе. Читав спектар се састоји од низа оштро одређених линија.
Лако је увидети да линијски спектар потиче од атома. Такви се спектри добијају при експериментима с катодним и каналним зрацима. Електрично избијање у катодној цеви ниског притиска изазива увек велики број атома на емисију светлости. Линијске спектре емитују такође и племенити гасови, који се састоје од чистих атома, а не молекула.
Линијски спектри се могу студирати на емисијском или апсорпционом спектру. Пусти ли се бела светлост кроз неке паре или плин, опажа се у добијеном спектру да су неке таласне дуљине угушене. Тамне линије стоје тачно на оним местима спектра где би лежале емисијске линије. Гас дакле апсорбује светлост оних таласних дужина које би иначе емитовао. Апсорпцијски спектар слаже се потпуно с емисионим. Ова одређеност у спектрима хемијских елемената један је од темељних закона нуклеарне физике.
Иако сваком хемијском елементу припадају посебне, својствене спектралне линије, ипак се у њиховим спектрима опажају нека заједничка својства, која омогућују да се унесе ред у голем спектроскопски материјал. Спектралне линије сваког хемијског елемента дају се средити у неколико серија. Свака поједина серија представља низ линија које су поређане по одређеном правилу. Често се већ на први поглед види да линије једне серије припадају заједно. Проматрају ли се линије од већих таласних дужина према мањим, непосредно је уочљиво да се размак између њих смањује. Линије се гомилају према одређеној таласној дужини, која је граница те серије.
Први је Ј. Ј. Балмер 1885. открио да се водоников спектар може приказати једноставном математичком једначиниом. Њему су тада биле познате 4 видљиве водоникове линије с таласним дужинама:
- Hα = 656, 199 nm
- Hβ = 486, 152 nm
- Hγ = 434, 067 nm
- Hδ = 410, 194 nm
Обичај је да се водоникове линије означе почетним словима грчког алфабета, која долазе као индекси хемијском симболу H. Реципрочне вредности таласних дужина те четири линије даје се једначином (Ридбергова формула):
где је: m = 3, 4, 5, 6; а R је такозвана Ридбергова константа. Уврсти ли се у Балмеровој једначини за м цели бројеви већи од 7 добијају се таласне дужине које леже у ултраљубичастом подручју спектра. Експериментима се заиста нашло још око 30 линија које се потпуно слажу с Балмеровом једначином. Линије се гомилају према таласној дужини која је дана изразом:
То је граница серије. Балмерова серија је идеални тип спектралних линија уопште. Како се види на слици, размак између суседних линија правилно се смањује, и линије се гомилају према одређеној граници.
Из разлога који ће се касније изнети уведено је да се спектралне једначине постављају за фреквенције, а не за таласне дужине. Експериментима се, додуше, мере таласне дужине (из интерферентних, дифракционих или дисперзионих појава), али закони спектралне анализе постају прегледнији кад се узимају у обзир фреквенције. При том треба мислити на следеће: фреквенција ν се може израчунати из таласне дуљине λ према познатом односу:
Но брзина светлости c није тако тачно измерена како су тачна мерења таласне дужине. Тачност спектралне анализе је ненадмашива. Из тог разлога и даље се у спектралној анализи сви искуствени подаци изражавају у таласним дужинама.
Уводећи фреквенцију, може се Балмерова једначина писати у облику:
где је m = 3, 4, 5…. Фреквенције спектралних линија водоника могу се дакле приказати као разлике (диференције) између два члана, од којих је први константан, а други опада као 1/9, 1/16, 1/25, 1/36 …. Ту се одмах намеће питање: Мора ли се увек узети као константан број 1/4? Могуће је помислити, да први константни члан буде било који разломак 1/n2. Godine 1908. našao je Ф. Пашен у инфрацрвеном подручју спектралне линије водоника којима су се таласне дужине тачно слагале с изразима:
Ту дакле постоје два члана једне серије, којој је константни члан R/32. Тај члан уједно одређује и границу серије. И од те такозване Пашенове серије нађен је врло велик број линија. Године 1916. пронашао је Лиман на другој страни од Балмерове серије, дубоко у ултраљубичастом подручју, нове спектралне линије, које се могу приказати истом Балмерововом једначином, само што се за константни члан требало узети у имениоцу цели број 1. Водоников спектар састоји се, од ових серија:
Лиманова серија:
где је: m = 2, 3, 4 ….
где је: m = 3, 4, 5 ….
Пашенова серија:
где је: m = 4, 5, 6 ….
Брацетова серија:
где је: m = 5, 6, 7 ….
Пфундова серија:
где је: m = 6, 7, 8 ….
Од тог големог мноштва линија падају у видљиво подручје спектра свега прве 4 линије Балмерове серије. Одатле се види како је важно испитивати читав спектар да се нађу основни закони серије.
Фреквенције спектралних линија водоника могу се генерално изразити једначином:
где су: n и m - цели бројеви.
Фреквенције водоникових линија добију се, дакле, да се од низа c∙R/n2 учине све могуће позитивне разлике (диференције). Тако објашњена, Балмерова једначина води нас до општег начела комбинације, што га је открио В. Риц 1908. По том начелу може се за сваки хемијски елемент поставити низ чланова T1, T2, T3, …. тако да су фреквенције његовог спектра дате разликама (диференцијама):
Рицово начело комбинације потврђено је при испитивању свих спектара. Оно је кључ за сређивање различитих серија. Начело комбинације садржи у себи основни закон природе, који се у пуном смислу разоткрива тек у нуклеарној физици.[7]
Референце[уреди | уреди извор]
- ^ „Johannes Robert Rydberg | Swedish physicist”. Encyclopedia Britannica (на језику: енглески). Приступљено 2021-02-02.
- ^ Šibalić, Nikola; S Adams, Charles (2018). Rydberg Physics (на језику: енглески). IOP Publishing. Bibcode:2018ryph.book.....S. ISBN 9780750316354. doi:10.1088/978-0-7503-1635-4.
- ^ Hamilton, Paul Charles (1992). Janne Rydberg: a physicist in 19th-century Sweden. [Cambridge, Massachusetts]. стр. 26—30.
- ^ Martinson, I.; Curtis, L.J. (2005). „Janne Rydberg – his life and work” (PDF). Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms (на језику: енглески). 235 (1–4): 17—22. Bibcode:2005NIMPB.235...17M. doi:10.1016/j.nimb.2005.03.137.
- ^ Hamilton (1992). Janne Rydberg: a physicist in 19th-century Sweden. стр. 47—48.
- ^ Rydberg, Johannes Robert , [1] "Hrvatska enciklopedi-ja", Leksikografski zavod Miroslav Krleža, enciklopedija.hr, 2017.
- ^ Ivan Supek: "Nova fizika", Školska knjiga Zagreb, 1966.
Литература[уреди | уреди извор]
- Mike Sutton, “Getting the numbers right – the lonely struggle of Rydberg” Chemistry World, Vol. 1, No. 7, July 2004.
- Martinson Indrek, L.J. Curtis: "Janne Rydberg – his life and work", journal = NIM B, [2] 2005.
- O'Connor, John J.; Robertson, Edmund F., "Johannes Rydberg", MacTutor History of Mathematics archive, University of St Andrews, [3].
- Magie, William Francis (1969). A Source Book in Physics. Cambridge, Massachusetts: Harvard University Press.
- Rydberg, J.R. (1889). „Researches sur la constitution des spectres d'émission des éléments chimiques” [Investigations of the composition of the emission spectra of chemical elements]. Kongliga Svenska Vetenskaps-Akademiens Handlingar [Proceedings of the Royal Swedish Academy of Science]. 2nd series (на језику: француски). 23 (11): 1—177.
- Rydberg, J.R. (1890). „On the structure of the line-spectra of the chemical elements”. Philosophical Magazine. 5th series. 29: 331—337.
- Litzén, Ulf (2015). Fysik i Lund under 300 år (на језику: шведски). Lund: Lunds universitetshistoriska sällskap. ISBN 9789175453200.
- Hamilton (1992). Janne Rydberg: a physicist in 19th-century Sweden.
- Martinson, I.; Curtis, L.J. (2005). „Janne Rydberg – his life and work” (PDF). Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms (на језику: енглески). 235 (1–4): 17—22. Bibcode:2005NIMPB.235...17M. doi:10.1016/j.nimb.2005.03.137.
Спољашње везе[уреди | уреди извор]
- O'Connor, John J.; Robertson, Edmund F. „Јоханес Ридберг”. MacTutor History of Mathematics archive. University of St Andrews.















