Пређи на садржај

Hablov zakon

С Википедије, слободне енциклопедије

Hablov zakon ili Habl—Lemetrov zakon[1] u fizičkoj kosmologiji je matematička formulacija tvrđenja da je brzina udaljavanja veoma udaljenih galaksija srazmerna njihovoj međusobnoj udaljenosti. U konkretnom slučaju, posmatrano sa naše planete, Zemlje, sve udaljene galaksije deluju kao da se od nas i naše galaksije udaljavaju brzinama koje su srazmerne njihovoj daljini, što se može zaključiti na osnovu crvenog pomaka frekvencije (ili talasne dužine) njihove svetlosti.[2][3] Ovaj zakon prvi su formulisali Edvin Habl (Edwin Hubble) i Milton Humason , 1929. godine,[4] nakon skoro cele decenije astronomskih osmatranja i merenja. Ovaj zakon smatra se prvom opservacionom osnovom za pretpostavku o metričkom širenju kosmosa i danas služi kao najviše pominjani deo dokaza u prilog kosmološkog modela velikog praska (engl. -Big Bang).

Hablov zakon se smatra prvom opservacionom osnovom za širenje svemira i danas služi kao jedan od dokaza koji se najčešće navode kao podrška modelu Velikog praska.[5][6] Kretanje astronomskih objekata isključivo zbog ovog širenja poznato je pod nazivom Hablov tok.[7] Ovaj zakon se često izražava jednačinom v = H0D, pri čemu je H0 konstanta proporcionalnosti — Hablova konstanta - između „odgovarajuće rastojanja” D do galaksije, koja se tokom vremena može menjati, za razliku od prateće razdaljine, i njene brzine odvajanja v, tj. derivata odgovarajuće udaljenosti u odnosu na kosmološku vremensku koordinatu. (Pogledajte upotrebu odgovarajuće udaljenosti za nekoliko diskusija o suptilnostima ove definicije 'brzine'.)

Hablova konstanta se najčešće navodi u (km/s)/Mpc, što daje brzinu u km/s za galaksiju koja je udaljena 1 Mpc (3,09×1019 km), a njena vrednost iznosi oko 70 (km/s)/Mpc. Međutim, SI jedinica za H0 je jednostavno s−1, a SI jedinica za recipročnu vrednost od H0 je sekunda. Recipročna vrednosti od H0 je poznata kao Hablovo vreme. Hablova konstanta se takođe može tumačiti kao relativna brzina ekspanzije. U ovom obliku H0 = 7%/Gyr, što znači da je pri trenutnoj stopi širenja potrebno milijardu godina da nevezana struktura naraste za 7%.

Iako se široko pripisuje Edvinu Hаlu,[8][9][10] pojam širenja svemira sa izračunljivom stopom prvi je izveo iz jednačina opšte relativnosti 1922. godine Aleksander Fredman. Fridman je objavio skup jednačina, sada poznatih kao Fridmanove jednačine, pokazujući da se svemir može proširiti i predstavivši brzinu širenja ako je to slučaj.[11] Zatim je Žorž Lemetr, u članku iz 1927. godine, nezavisno zaključio da se svemir može širiti, uočio proporcionalnost između recesione brzine i udaljenosti do udaljenih tela, i predložio procenjenu vrednost konstante proporcionalnosti, koja je nakon Hablove korekcije postala poznata kao Hablova konstanta.[5][12][13][14] Štaviše, dve godine kasnije, Edvin Habl je potvrdio postojanje kosmičke ekspanzije i odredio tačniju vrednost za konstantu koja sada nosi njegovo ime.[15] Habl je izveo recesionu brzinu objekata iz njihovih crvenih pomaka, mnoge od kojih je ranije izmerio i povezao sa brzinom Vesto Slajfer 1917. godine.[16][17][18] Iako je Hablova konstanta približno konstantna u prostoru brzine-rastojanja u bilo kojem trenutku u vremenu, Hablov parametar , za koji Hablova konstanta daje trenutnu vrednost, varira s vremenom, tako da se termin 'konstanta' ponekad smatra u izvesnom smislu pogrešnim nazivom.[19][20]

Otkriće

[уреди | уреди извор]

U deceniji pre nego što je Habl vršio svoja osmatranja, veći broj fizičara i matematičara postavili su konzistentnu teoriju koja daje vezu između prostora i vremena, koristeći Ajnštajnove jednačine polja iz opšte relativnosti. Primenjujući na pitanje prirode svemira većinu opšte-relativističkih principa došli su do rešenja koje bilo u suprotnosti sa dotada preovlađujućom predstavom o statičnosti svemira.

Godine 1922, ruski naučnik Aleksandar Fridman izveo je, na osnovu Ajnštajnovih jednačina polja, svoje ili Fridmanove jednačine, pokazujući na taj način da bi svemir možda mogao da se širi i izračunavajući brzinu širenja u slučaju ako je to tačno.[21]. Parametar koji je Fridman za to koristio danas je poznat kao skalarni faktor, koji se može shvatiti kao skalarno invarijantni oblik konstante proporcionalnosti Hablovog zakona. Žorž Lemetr je 1927. godine, nezavisno od Fridmana, našao slično rešenje i predstavio ga u jednom svom radu. Ove Fridmanove i Lemetrove ideje verovatno su svojevremeno dovele i do stvaranja, danas preovlađujuće, teorije velikog praska.

Pre nastupanja moderne kosmologije, vodila se prilično velika rasprava oko toga kolika je veličina svemira i kakav je njegov oblik. U 1920. godini uzela je maha čuvena debata na ovu temu između Harloa Šejplija (Harlow Shapley) i Herberta D. Kertisa (Heber D. Curtis), u kojoj se Šejpli zalagao za mali svemir, veličine naše galaksije Mlečni put, a Kertis je tvrdio da je svemir mnogo veći od toga. Ovo pitanje bilo je razrešeno u nadolazećoj deceniji sa poboljšanjima u opažanju kosmosa koja su donela Hablova astronomska osmatranja. Edvin Habl je većinu svog profesionalnog rada na astronomskim osmatranjima učinio na opservatoriji Maunt Vilson, (Mount Wilson observatory), koja je imala u to vreme najveći teleskop na svetu. Njegova osmatranja promenljivih zvezda, Cefeida, u spiralnim galaksijama omogućila su mu da izračuna udaljenost do tih kosmičkih objekata. Na njegovo iznenađenje, udaljenost ovih objekata bila je toliko velika da bi oni trebalo da budu smešteni poprilično daleko izvan našeg Mlečnog puta. Ove zvezdane nebule (grupacije) najpre su opisane kao “svemirska ostrva”, da bi tek kasnije dobile naziv galaksije.

Kombinujući njegova merenja udaljenosti galaksija sa Vesto Sliperovim (Vesto Slipher) merenjima crvenog pomaka njihove svetlosti, Habl je otkrio grubu proporcionalnost između ovo dvoje. Mada je postojalo poprilično rasipanje mernih podataka (danas se zna da je to bilo izazvano drugim, neregularnim, brzinama, ovih objekata), on je bio u stanju da povuče pravu liniju na grafiku zavisnosti brzina od udaljenosti za 46 galaksija koje je proučavao i tako dobije vrednost Hablove konstante koja iznosi 500 km/s/Mpc (500 km/s po megaparseku), što je mnogo više od danas prihvaćene vrednosti, zahvaljujući greškama u kalibraciji udaljenosti, što je veoma čest problem čak i za današnje astronome.

U 1958. prva dobra procena Hablove konstante, od 75 km/s/Mpc, napravljena je od strane Alana Sandejdža (Allan Sandage), ali potrebne su bile još decenije da bi se oko toga postigao konsenzus.

Objašnjenje

[уреди | уреди извор]

Otkriće linearne (direktne) zavisnosti između brzine udaljavanja i udaljenosti galaksija, dobilo je odmah zatim matematički izraz u Hablovom zakonu, datom sa:

Gde je brzina udaljavanja koja je u skladu sa opaženim crvenim pomakom, uobиčajeno izražena u km/s. je Hablova konstanta koja je u vezi sa vrednošću (obično nazvanoj Hablov parametar, koji je vremenski zavisan), koja se u Fridmanovim jednačinama u datom trenutku opažanja obeležava indeksom “0”. Ova vrednost je jednaka kroz ceo svemir za dato konformalno vreme. je odgovarajuća udaljenost koju svetlost prelazi polazeći od udaljene galaksije do posmatrača, merena u referentnom sistemu posmatrača i izražena u mega parsecima, Mpc.

Za relativno bliske galaksije, brzina “” može se približno odrediti iz galaksijinog crvenog pomaka, korišćenjem formule , gde je “” brzina svetlosti. Za veoma udaljene galaksije, “” mora da se određuje iz crvenog pomaka “” na osnovu “relativističkog doplerovog efekta jer bi tada brzine udaljavanja galaksija trebalo da budu bliske brzini svetlosti. Ipak, najbolji način da se proračunaju brzine udaljavanja koje su u vezi sa povećanjem brzine širenja prostor-vremena je da se uzme u razmatranje konformalno vreme povezano sa putovanjem fotona sa udaljenih galaksija. U tom slučaju dobija se da brzina udaljavanja “” za veoma udaljene objekte može da bude i veća od brzine svetlosti “”, što ne bi trebalo da ugrožava specijalnu relativnost ako se uzme u obzir da brzina metričke ekspanzije svemira nije u vezi sa brzinom bilo kojeg fizičkog objekta.

Prilikom korišćenja Hablovog zakona za određivanje udaljenosti, samo brzine koje su posledica širenja svemira treba da se koriste. Pošto se galaksije koje međusobno gravitaciono interaguju kreću jedna u odnosu na drugu nezavisno od širenja svemira, ove relativne brzine, nazvane “specifične brzine” (engl. -“peculiar velocities”), treba takođe da se uzmu u obzir kada se u takvim slučajevima primenjuje Hablov zakon. Efekat pod nazivom “Božiji prst” (engl. - Finger of God) je jedan od rezultata ove pojave koju je otkrio 1938. Bendžamin Keneli (Benjamin Kenneally). Sistemi koji su gravitaciono povezani, kao neke galaksije, ili nebeska tela u našem planetarnom sistemu, nisu uključeni u Hablov zakon i oni se ne šire.

Matematičko izvođenje idealizovanog Hablovog zakona za uniformno širenje kosmosa je prilično elementarna teorema iz 3-dimenzionalnog, kartezijanskog, koordinatnog prostora, koji se shvata kao metrički prostor koji je u potpunosti homogen i izotropan, odnosno njegova svojstva se ne menjaju ni u različitim tačkama ni u različitim pravcima. Jedan jednostavan izraz ove teoreme je sledeći:

“Bilo koje dve tačke koje se kreću iz zajedničkog početka, svaka duž prave linije i sa brzinom srazmernom udaljenosti od početka, udaljavaće se i međusobno sa brzinom srazmernom njihovoj međusobnoj udaljenosti.

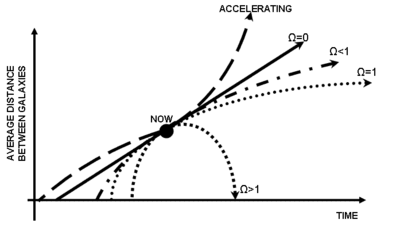
Konačna sudbina svemira i starost svemira mogu se odrediti današnjim merenjem Hablove konstante i ekstrapolacijom sa opaženom vrednošću parametra usporenja (deceleracije) jednoznačno okarakterisanog preko vrednosti parametra gustine (Ω). Takozvani “zatvoreni svemir” (Ω>1) dolazi do svoga kraja velikim smrskavanjem (engl. Big Crunch). i on je značajno mlađi od Hablovog vremena (recipročna Hablova konstanta). “Otvoreni svemir” (Ω≤1) širi se zauvek i njegova starost je bliska Hablovom vremenu. Za ubrzavajući svemir kojem bi trebalo mi da pripadamo, starost bi trebalo da bude veoma bliska Hablovom vremenu.
Konačna sudbina svemira i starost svemira mogu se odrediti današnjim merenjem Hablove konstante i ekstrapolacijom sa opaženom vrednošću parametra usporenja (deceleracije) jednoznačno okarakterisanog preko vrednosti parametra gustine (Ω). Takozvani “zatvoreni svemir” (Ω>1) dolazi do svoga kraja velikim smrskavanjem (engl. Big Crunch). i on je značajno mlađi od Hablovog vremena (recipročna Hablova konstanta). “Otvoreni svemir” (Ω≤1) širi se zauvek i njegova starost je bliska Hablovom vremenu. Za ubrzavajući svemir kojem bi trebalo mi da pripadamo, starost bi trebalo da bude veoma bliska Hablovom vremenu.

Vrednost Hablovog parametra trebalo bi da se menja tokom vremena, bilo da raste ili se smanjuje, zavisno od znaka tzv. parametra usporavanja (deceleration parameter) koji je definisan sa:

U svemiru sa parametrom usporavanja koji je jednak nuli, sledi da je H = 1/t, gde je t vreme proteklo od velikog praska. Ne-nulta vrednost od jednostavno zahteva integriranje Fridmanovih jednačina unazad od sadašnjeg vremena do vremena kada je veličina svemira bila jednaka nuli.

Može da se definiše i “Hablovo doba” (takođe poznato i kao “Hablovo vreme” ili “Hablov period”) svemira kao 1/H, ili 977793 miliona godina. Za Hablovo doba dobija se 13968 miliona godina ako se uzme vrednost H=70 km/s/Mpc, ili 13772 miliona godina za vrednost H=71 km/s/Mpc. Udaljenost galaksija dobija se približno kao zc/H za male vrednosti crvenog pomaka “z”, a izražavanjem “c” kao jedne svetlosne godine po godini ova udaljenost može se još jednostavnije izraziti kao “z” pomnoženo sa milion svetlosnih godina.

Dugo vremena je vladalo mišljenje da je “q” pozitivno, što bi značilo da se širenje svemira usporava zahvaljujući gravitacionom privlačenju. Iz ovoga proizilazi da je starost svemira manja od 1/H (što je oko 14 milijardi godina). Na primer, vrednost za “q” od ½ (jedna teorijska mogućnost) dalo bi vrednost za starost svemira od 2/(3H). Otkriće iz 1998 godine da je q kako izgleda negativno, znači da je svemir u stvari stariji od 1/H. U stvari, nezavisne procene starosti svemira dolaze do vrednosti koja je prilično bliska sa 1/H.

Reference

[уреди | уреди извор]
  1. ^ „IAU members vote to recommend renaming the Hubble law as the Hubble–Lemaître law” (Саопштење). International Astronomical Union. 29. 10. 2018. Приступљено 29. 10. 2018. 
  2. ^ Riess, A.; et al. (1998). „Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant”. The Astronomical Journal. 116 (3): 1009—1038. Bibcode:1998AJ....116.1009R. arXiv:astro-ph/9805201 Слободан приступ. doi:10.1086/300499. 
  3. ^ Perlmutter, S.; et al. (1999). „Measurements of Omega and Lambda from 42 High-Redshift Supernovae”. The Astrophysical Journal. 517 (2): 565—586. Bibcode:1999ApJ...517..565P. arXiv:astro-ph/9812133 Слободан приступ. doi:10.1086/307221. 
  4. ^ Hubble, Edwin (1929). „A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae”. Proceedings of the National Academy of Sciences of the United States of America. 15 (3): 168—173.  (Full article |url=http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1929PNAS...15..168H&db_key=AST&data_type=HTML&format=&high=42ca922c9c30954 [https://web.archive.org/web/20080630010328/http://www.pnas.org/cgi/reprint/15/3/168 Архивирано на сајту Wayback Machine (30. јун 2008), PDF)
  5. ^ а б Overbye, Dennis (20. 2. 2017). „Cosmos Controversy: The Universe Is Expanding, but How Fast?”. New York Times. Приступљено 21. 2. 2017. 
  6. ^ Coles, P., ур. (2001). Routledge Critical Dictionary of the New Cosmology. Routledge. стр. 202. ISBN 978-0-203-16457-0. 
  7. ^ „Hubble Flow”. The Swinburne Astronomy Online Encyclopedia of Astronomy. Swinburne University of Technology. Приступљено 14. 5. 2013. 
  8. ^ van den Bergh, S. „The Curious Case of Lemaitre's Equation No. 24”. Journal of the Royal Astronomical Society of Canada. 105 (4): 151. Bibcode:2011JRASC.105..151V. arXiv:1106.1195 Слободан приступ. 
  9. ^ Nussbaumer, H.; Bieri, L. „Who discovered the expanding universe?”. The Observatory. 131 (6): 394—398. Bibcode:2011Obs...131..394N. arXiv:1107.2281 Слободан приступ. 
  10. ^ Way, M.J. „Dismantling Hubble's Legacy?”. ASP Conference Proceedings. 471: 97—132. Bibcode:2013ASPC..471...97W. arXiv:1301.7294 Слободан приступ. 
  11. ^ Friedman, A. (decembar 1922). „Über die Krümmung des Raumes”. Zeitschrift für Physik. 10 (1): 377—386. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. . (English translation in. )
  12. ^ Lemaître, G. (1927). „Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques”. Annales de la Société Scientifique de Bruxelles A. 47: 49—59. Bibcode:1927ASSB...47...49L.  Partially translated in Lemaître, G. (1931). „Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulae”. Monthly Notices of the Royal Astronomical Society. 91 (5): 483—490. Bibcode:1931MNRAS..91..483L. doi:10.1093/mnras/91.5.483. 
  13. ^ Livio, M. (2011). „Lost in translation: Mystery of the missing text solved”. Nature. 479 (7372): 171—3. Bibcode:2011Natur.479..171L. PMID 22071745. doi:10.1038/479171a. 
  14. ^ Livio, M.; Riess, A. (2013). „Measuring the Hubble constant”. Physics Today. 66 (10): 41. Bibcode:2013PhT....66j..41L. doi:10.1063/PT.3.2148. 
  15. ^ Hubble, E. (1929). „A relation between distance and radial velocity among extra-galactic nebulae”. Proceedings of the National Academy of Sciences. 15 (3): 168—73. Bibcode:1929PNAS...15..168H. PMC 522427 Слободан приступ. PMID 16577160. doi:10.1073/pnas.15.3.168. 
  16. ^ Slipher, V.M. (1917). „Radial velocity observations of spiral nebulae”. The Observatory. 40: 304—306. Bibcode:1917Obs....40..304S. 
  17. ^ Longair, M. S. (2006). The Cosmic CenturyНеопходна слободна регистрација. Cambridge University Press. стр. 109. ISBN 978-0-521-47436-8. 
  18. ^ Nussbaumer, Harry (2013). 'Slipher's redshifts as support for de Sitter's model and the discovery of the dynamic universe' In Origins of the Expanding Universe: 1912-1932. Astronomical Society of the Pacific. стр. 25—38. arXiv:1303.1814 Слободан приступ. 
  19. ^ Overbye, Dennis (25. 2. 2019). „Have Dark Forces Been Messing With the Cosmos? - Axions? Phantom energy? Astrophysicists scramble to patch a hole in the universe, rewriting cosmic history in the process.”. The New York Times. Приступљено 26. 2. 2019. 
  20. ^ O'Raifeartaigh, Cormac (2013). The Contribution of V.M. Slipher to the discovery of the expanding universe in 'Origins of the Expanding Universe'. Astronomical Society of the Pacific. стр. 49—62. arXiv:1212.5499 Слободан приступ. 
  21. ^ Friedman, A: Über die Krümmung des Raumes, Zeitschrift für Physik. 10  377-386. (English translation in: General Relativity and Gravitation. 31  1991-2000.)

Literatura

[уреди | уреди извор]

Spoljašnje veze

[уреди | уреди извор]
Hablov zakon на Викимедијиној остави.
Преузето из „https://sr.wikipedia.org/w/index.php?title=Hablov_zakon&oldid=28520896”