Kulonov zakon

| Elektromagnetizam |
|---|
 |
U fizici, Kulonov zakon definiše intenzitet, pravac i smer elektrostatičke sile kojom nepokretno naelektrisanje malih dimenzija deluje na drugo. Ta sila se često naziva i Kulonova sila. Nazvana je po francuskom fizičaru Šarlu Kulonu koji je koristio torzionu vagu kako bi je izmerio. Zakon glasi:
Intenzitet elektrostatičke sile između dva tačkasta naelektrisanja je direktno proporcionalan proizvodu količina njihovih naelektrisanja, a obrnuto proporcionalan kvadratu rastojanja između ta dva naelektrisanja.
Istorija[uredi | uredi izvor]
Drevne kulture širom Mediterana su znale da pojedini objekti, kao što su šipke od ćilibara, pri trljanju sa mačjim krznom mogu da privuku lake predmete poput perja. Tales iz Mileta je 600 godina pre nove ere vršio oglede vezane za statički elektricitet. Iz proučavanja je zaključio da neki materijali, kao mineral magnetita, sami pokazuju magnetne osobine, dok je neke materijale da bi pokazali magnetne osobine potrebno prethodno utrljati, te da se tako ćilibar namagnetisava utrljavanjem, tj. trenjem. Tales je pogrešio verujući da se privlačnost događa zbog magnetnog dejstva, jer će kasnije nauka dokazati vezu između magnetizma i elektriciteta.

Struja će ostati nešto više od intelektualne radoznalosti milenijumima, sve do 1600. godine, kada je engleski naučnik Vilijam Gilbert uspeo pažljivim proučavanjem elektriciteta i magnetizma, da napravi razliku između magnetizma i statičkog elektriciteta proizvedenog trljanjem ćilibarom. On je izmislio novu latinsku reč lectricus (u direktnom prevodu od ćilibara ili poput ćilibara, iz grčke reči za ćilibar ηλεκτρον [elektron]). Ta reč se odnosila na osobinu privlačenja malih objekata nakon trenja. To je asociralo Tomasa Brauna da u svojoj knjizi „Pseudodoxia Epidemica“ 1646. godine po prvi put u istoriji koristi engleske reči električni i struja.
Pojedini naučnici sa početka 18. veka su sumnjali da električna sila, poput gravitacione, se smanjuje sa distancom (tj., da je obrnuto srazmerna kvadratu rastojanja) uključujući Danijela Bernulija i Alesandra Volta. Obojica su merila silu između ploče kondenzatora, a Franc Epinus koji je objavio inverzno-kvadratni zakon u 1758. godini.
Na osnovu eksperimenata na naelektrisanim sferama, Džozef Pristli u Engleskoj bio je među prvima koji predlaže da električna snaga prati inverzno-kvadratni zakon, sličan Njutnovom zakonu univerzalne gravitacije. Međutim, on nije generalizovao ili razradio ovo. U 1767. godini, on je pretpostavio da sila između dva punjenja varira kao obrnutom kvadratu rastojanja.

U 1769, škotski fizičar Džon Robison je najavio da, prema njegovim merenjima, sila odbijanja između dve sfere sa istim znakom varira kao x -2.06.
Početkom 1770-ih godina, zavisnost sile između naelektrisanih tela na obe distance i punjenja već je bilo otkriveno, ali nije objavljeno, po Henriju Kevendišu iz Engleske.
Konačno, 1785te godine, francuski fizičar Šarl-Ogisten de Kulon je objavio svoja prva tri izveštaja o elektricitetu i magnetizmu, gde je izneo svoj zakon. Ova publikacija je od suštinskog značaja za razvoj teorije elektromagnetizma. On je koristio torzionu vagu za proučavanje odbojne i privlačne sile naelektrisanih čestica, i utvrdio da je veličina električne sile između dve ključne tačke punjenja direktno proporcionalna proizvodu punjenja i obrnuto proporcionalna kvadratu rastojanja između njih.
Torziona vaga sastoji se od šipke zakačena kroz svoju sredinu tankim vlaknima. Vlakna deluje kao jako slaba torziona opruga. U Kulonovom eksperimentu, torziona vaga je izolacioni štap sa loptom sa metalnom košuljicom na jednog kraja zakačena svilenim koncem. Lopta je bila naelektrisana sa poznatim naelektrisanjem za statički elektricitet, a druga naelektrisana lopta istog polariteta je doveden do nje. Dve naelektrisane kugle su se odbile jedna od druge, uvrćući vlakna pod određenim uglom, koji se može očitati sa skale na instrumentu.
Znajući kolika je sila potrebna da se uvrnu vlakana do datog ugla, Kulon je uspeo da izračuna sile između kugli i izvede svoj inverzno-kvadrati proporcionalni zakon.
Zakon[uredi | uredi izvor]
Kulonov zakon navodi da:
- Intenzitet elektrostatičke sile između dva tačkasta naelektrisanja je direktno proporcionalan proizvodu količina njihovih naelektrisanja, a obrnuto proporcionalan kvadratu rastojanja između ta dva naelektrisanja.

Kulonov zakon se može navesti kao jednostavan matematički izraz. Skalarni i vektorski oblici matematičke jednačine su
| i | , |
gde je ke Kulonova konstanta, q1 i q2 su magnitude naelektrisanja, skalarno r je rastojanje između naelektrisanja, vektor je vektorsko rastojanje između naelektrisanja i (Jedinični vektor od q2 do q1). Vektorski oblik jednačine iznad izračunava silu primenjuje na q1 od strane q2. Ako je r12 umesto toga iskorišćen, onda se efekat na q2 može naći. Takođe se može izračunati korišćenjem Njutnovog trećeg zakona : .
Jedinice[uredi | uredi izvor]
Elektromagnetna teorija obično se izražava pomoću Međunarodnog sistema jedinica. Sila se meri u njutnima, naelektrisanje u kulonima, i udaljenost u metrima. Kulonova konstanta je data sa . Konstanta je dielektrična konstanta slobodnog prostora u C2 m−2 N−1. I je relativna dielektrična konstanta materijala u koji je uronjeno naelektrisanje, pa je bezdimenziona. U Međunarodnom sistemu izvedenih jedinica za električno polje je volt po metru, Njutn po Kulonu, ili tesla metara u sekundi. Kulonov zakon i Kulonova konstanta može se tumačiti u različitim uslovima:
- atomska jedinica. U atomskim jedinicama snaga se izražava u Hartreeju po Bohraovom radijusu, naelektrisanje u smislu osnovnog naelektrisanja, i daljina u smislu Bohrovog radijusa.
- elektrostatičke jedinice ili Gausove jedinice. U elektrostatičke jedinice i Gausova jedinica, jedinica punjenje se definiše na takav način da Kulonova konstanta k nestaje jer ima vrednost jednog i postaje bezdimenziona .
Električno polje[uredi | uredi izvor]
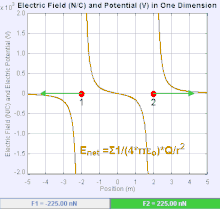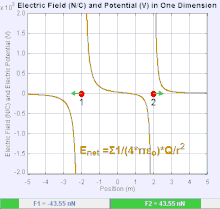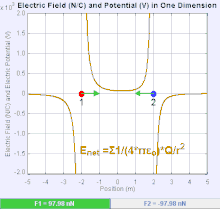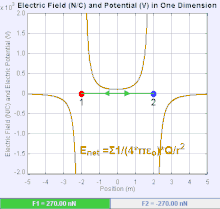
Električno polje je vektorsko polje koje povezuje svaku tačku u prostoru Kulonovih sila kroz koji prolazi test naelektrisanja. U najjednostavnijem slučaju, smatra se da će biti generisan od strane isključivo jednog izvora naelektrisane tačke. Snaga i pravac sile Kulona na test naelektrisanja zavisi od električnog polja da se nađe u njemu, tako da je . Ako se polje generiše pozitivno naelektrisanom izvornom tačkom , smer električnog polja tačaka duž linija usmerenih radijalno ka spolja od njega, odnosno u smeru pozitivnom naboju tačka testa pomerilo bi se ako je stavljeno na polje. Za negativno naelektrisani izvor naelektrisanja, pravac je radijalno ka unutra.
Veličina električnog polja se može izvesti iz Kulonovog zakona. Izborom jedne od tačaka naelektrisanja da je izvor, a drugi da bude test punjenja, prati da je iz Kulonovog zakona veličina ovog električnog polja napravljen od strane jednog izvora naelektrisane tačka na određenoj udaljenosti od njega u vakuumu daje:
- .
Kulonova konstanta[uredi | uredi izvor]
Kulonov konstanta proporcionalnosti je faktor koji se pojavljuje u Kulonovom zakonu, kao i u drugim elektro-srodnih formula. Označava , poznata kao konstantna električne sile ili elektrostatička konstanta, pa indeksni .
Tačna vrednost Kulonove konstante je:
Stanje punovažnosti[uredi | uredi izvor]
Postoje dva uslova koje treba ispuniti za važenja Kulonovog zakona:
- Razmatrana naelektrisanje moraju biti deo tačke naelektrisanja.
- Oni treba da budu stacionarne u međusobnom odnosu jedna na drugu.
Skalarni oblik[uredi | uredi izvor]

Kada je to samo od interesa da se zna veličina elektrostatičke sile (a ne njegov smer), je lakše da se razmotri skalarni oblik zakona. Skalarni oblik Kulonovog zakona se odnosi na obim i znak elektrostatičke sile koja deluje istovremeno na dve tačke optužnice i na sledeći način:
gde je rastojanje i Kulonova konstanta. Ako je proizvod pozitivan, sila između dva naelektrisanja je odbojna, a ako je proizvod negativan, sila između njih je privlačna.
Vektorski oblik[uredi | uredi izvor]

Kulonov zakon kaže da se elektrostatička sila na koje utiče naelektrisanje, na poziciji , u blizini drugog naelektrisanja, na poziciji , u vakuumu je jednaka:
Gde je , jedinični vektor , i električni konstanta .
Vektorski oblik Kulonovog zakona je jednostavna skalarna definicija zakona sa datim pravcem od vektorske jedinice, , paralelno sa linijom od naelektrisanja do naelektrisanja . Ako oba naelektrisanja imaju isti znak onda je proizvod pozitivan i pravac sile na je dat od strane ; Naelektrisanja odbijaju jedni druge. Ako naelektrisanja imaju suprotne znake onda proizvoda je negativan i pravac sile je dat od strane ;Naelektrisanja privlače jedni druge.
Elektrostatička sila na koje utiče naelektrisanje , prema trećem Njutnovom zakonu, je .
Sistem izolovanih naelektrisanja[uredi | uredi izvor]
Zakon poklapanja Kulonovom zakonu dozvoljava da bude proširen na bilo koji broj tačaka naelektrisanja. Sila koja deluje na tačku naelektrisanja, zbog toga sto je sistema tačaka naelektrisanja jednostavno vektorsko dodavanje pojedinačnih sila koje deluju samo na tačku naelektrisanja zbog svakog naelektrisanja. Rezultat je vektor sila paralelna sa električnim poljem vektora u tom trenutku, s uklonjenom tačkom naelektrisanja.
Sila na malom naelektrisanju , na poziciji , zbog sistema izolovano naelektrisanje u vakuumu je:
Gde su i veličina i položaj, u odnosno na naelektrisanja, je jedinični vektor u pravcu (Vektor pokazuje na osnovno naelektrisanje od do )).
Neprekidna raspodela naelektrisanja[uredi | uredi izvor]
U ovom slučaju, princip linearne superpozicije se takođe koristi. Za neprekidnu raspodelu naelektrisanja, integral celom regionu koji sadrži naelektrisanje odgovara beskonačnom zbiru, tretirajući svaki infinitezimalni element prostora kao tačka naelektrisanja . Raspodela naelektrisanja je obično linearna, površinska ili zapreminska.
Za linearnu raspodelu naelektrisanja (dobra aproksimacija za naelektrisanje u žice), gde daje naelektrisanje po jedinici dužine na poziciji , i je infinitezimalni element dužine,
- .
Za raspodelu površinskog naelektrisanja, gde daje naelektrisanje po jedinici površine, na poziciji i je infinitezimalni element prostora,
Za raspodelu zapreminskog naelektrisanja (kao što su naelektrisanje u okviru rasutih metala), gde daje naelektrisanje po jedinici zapremine, na poziciji , i je infinitezimalni element zapremine,
Sila na mali test naelektrisanja na poziciji u vakuumu dat od strane integrala preko raspodele naelektrisanja:
Jednostavan eksperiment za proveru Kulonovog zakona[uredi | uredi izvor]
Moguće proveriti Kulonov zakon sa jednostavnim eksperimentom. Razmotrimo dve male sfere mase i istim znakom naelektrisanja , koje visi o dva užeta zanemarljive mase dužine . Tri sile koje deluju na svaku sferi su: težina , zategnutost konopca i električne sile .
U stanju ravnoteže:
|
|
(1) |
i:
|
|
(2) |
Deljenjem (1) sa (2):
|
|
(3) |
Ako je rastojanje između naelektrisanih sferama, onda je odbojna sila između njih , pod pretpostavkom da je Kulonov zakon tačno, je jednaka
|
|
(Kulonov zakon) |
tako da je:
|
|
(4) |
Ako sada razelektrišemo jednu od sfera, a stavimo je u kontaktu sa naelektrisanom sferom, svaki od njih dobija naelektrisanje q/2. U stanju ravnoteže, rastojanje između naelektrisanja će biti i odbojnost sila između njih će biti:
|
|
(5) |
Znamo da je . I:
Deljenjem (3) sa (4), dobijamo:
|
|
(6) |
Merenjem uglove i i rastojanje između naelektrisanja i moguće je proveriti da jednakost važi, uzimajući u obzir eksperimentalnu grešku. U praksi, uglovi mogu biti teško izmerivi, pa ako je dužina užeta dovoljno velika, uglovi će biti dovoljno mali da bi se dobila sledeća aproksimacija:
|
|
(7) |
Koristeći ovu aproksimaciju, odnos (6) postaje mnogo jednostavniji izraz:
|
|
(8) |
Na ovaj način, verifikacija je ograničena na merenje rastojanja između naelektrisanja i provera da li je podela aproksimira teorijsku vrednost.
Elektrostatičke aproksimacije[uredi | uredi izvor]
U obema formulacijama, skalarnoj i vektorskoj, Kulonov zakon je tačan samo ako su naelektrisanja u mirovanju, a ostaje približno tačan za manje brzine kretanja. Kada se naelektrisanja kreću, stvara se magnetsko polje koje menja Kulonove sile koje deluju na naelektrisanja. Sila koja nastaje usled magnetskog polja može se smatrati kao sila elektrostatičkog polja pod uslovom da se u obzir uzme i Ajnštajnova teorija relativiteta.
Vidi još[uredi | uredi izvor]
Literatura[uredi | uredi izvor]
- Coulomb, Charles Augustin (1788) [1785]. „Premier mémoire sur l’électricité et le magnétisme”. Histoire de l’Académie Royale des Sciences. Imprimerie Royale. str. 569—577.
- Coulomb, Charles Augustin (1788) [1785]. „Second mémoire sur l’électricité et le magnétisme”. Histoire de l’Académie Royale des Sciences. Imprimerie Royale. str. 578—611.
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd izd.). Prentice Hall. ISBN 978-0-13-805326-0.
- Tipler, Paul A.; Mosca, Gene (2008). Physics for Scientists and Engineers (6th izd.). New York: W. H. Freeman and Company. ISBN 978-0-7167-8964-2. LCCN 2007010418.
- Young, Hugh D.; Freedman, Roger A. (2010). Sears and Zemansky's University Physics : With Modern Physics (13th izd.). Addison-Wesley (Pearson). ISBN 978-0-321-69686-1.
Spoljašnje veze[uredi | uredi izvor]
- MISN-0-114 Kulonov zakon od J. Kovač za Project PHYSNET.
- Coulomb's Law on Project PHYSNET
- Electricity and the Atom Arhivirano na sajtu Wayback Machine (21. februar 2009)—a chapter from an online textbook
- A maze game for teaching Coulomb's Law—a game created by the Molecular Workbench software
- Electric Charges, Polarization, Electric Force, Coulomb's Law Walter Lewin, 8.02 Electricity and Magnetism, Spring 2002: Lecture 1 (video). MIT OpenCourseWare. License: Creative Commons Attribution-Noncommercial-Share Alike.











































































![{\displaystyle {\frac {L_{1}}{L_{2}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Longrightarrow {\frac {L_{1}}{L_{2}}}\approx {\sqrt[{3}]{4}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c9166e7d5f120fd7a63a5c035838dbe36df9dcf)