Univerzalni zakon gravitacije

Matematičar i fizičar Isak Njutn u periodu od 1665. do 1685, razvio je svoju teoriju mehanike, zasnovanu na ubrzanju, a ne samo na proučavanju brzine, kako su to činili Galilej i Dekart pre njega. Ključna činjenica koju je Njutn prvi zapazio je da je sila koja deluje na jabuku koja pada sa drveta zapravo ista sila koja deluje na Zemlju da se okreće oko Sunca. Iz tog saznanja potekao je Njutnov zakon gravitacije, tj. univerzalni zakon gravitacije, koji se ubraja u četvrti Njutnov zakon, pored 3 osnovna zakona klasične mehanike. Univerzalni zakon gravitacije je formulisan u Njutnovom delu Philosophiæ Naturalis Principia Mathematica, koje je prvu put bilo objavljeno 5. jula 1687. Kad je Njutn predstavio Knjigu 1 neobjavljenog teksta u aprilu 1686. Kraljevskom društvu, Robert Huk je tvrdio da je Njutn dobio zakon inverznog kvadrata od njega.

U današnjem jeziku, zakon navodi da svaka tačka mase privlači svaku drugu tačku mase sa silom koja deluje duž linije koja spaja tačke. Sila je proporcionalna proizvodu dve mase, i inverzno proporcionalna kvadratu rastojanja između njih.

Formulacija zakona

${\vec {F}}_{12}=-G\cdot {\frac {m_{1}m_{2}}{d^{2}}}{\vec {u}}_{12}$

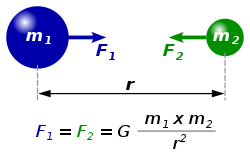
Gravitaciona sila kojom se privlače tela 1 i 2 srazmerna je proizvodu njihovih masa $m_{1}$ i $m_{2}$, a obrnuto> srazmerna kvadratu njihovog rastojanja, $d^{2}$.

$G$, je gravitaciona konstanta koja iznosi $6.67\cdot 10^{-11}{\frac {N\cdot m^{2}}{kg^{2}}}$ (ili ${\frac {m^{3}}{kg\cdot s^{2}}}$), a ${\vec {u}}_{12}$ je jedinični vektor usmeren od tela 1 prema telu 2. Negativni predznak označava da je sila među telima privlačna sila.

Dokaz

Drugi Njutnov zakon:

Osnovni zakon dinamike, tj. Drugi Njutnov zakon, koji polazi od Dekartovog principa inercije (održanje količine kretanja), pokazuje da zbirno delovanje sila na tela jednako $ma$, gde je $m$ inertna masa (koja otežava kretanje tela), i gde je $a$ ubrzanje (ritam promene brzine).

Uobičajenim nazivima rečeno:

Veličina sile na neko telo direktno je srazmerna ubrzanju i masi tog tela.

${\overrightarrow {F}}=m\cdot {\overrightarrow {a}}$

gde je F sila, m masa, a ubrzanje.

Keplerovi zakoni i Zakon o centrifugalnoj sili:

S druge strane, iz Keplerovih zakona, koji su izvedeni iz posmatranja kretanje tela u Sunčevom sistemu, i zakona Kristijana Hajgensa o centrifugalnoj sili, Njutn je zaključio da gravitaciona sila između dva tela deluje po pravoj liniji između njih i obrnuto je proporcionalna kvadratu njihovog rastojanja, tj. srazmerna je sa ${\frac {1}{d^{2}}}$, gde je $d$ rastojanje između tela.

Gravitaciona konstanta

Smatrajući da je sila gravitacije proporcionalna količini materije prisutnoj u telu koja deluju ovom silom (dvostruko veće telo deluje dvostruko većom silom), pertpostavio je da je sila proporcionalna veličini $m_{G}$ koju je nazvao gravitaciona masa, proporcionalna količini materije u telu i njegovoj sposobnosti da vrši privlačno delovanje.

Treći Njutnov zakon:

Po principu akcije i reakcije, sila kojom drugo telo deluje na prvo je jednaka (i usmerena u suprotnom smeru) sili kojom prvo telo deluje na drugo. Ova sila je proporcionalna $m'_{G}$, gravitacionoj masi drugog tela.

Zaključak:

Njutn je želeo da objedini zakone koji važe na Zemlji sa onima koji važe na nebu (astronomija), naročito one koji se odnose na Zemljinu težu i kretanje planeta).

Osnovni zakon dinamike se stoga može zapisati kao: $ma=G\cdot {\frac {m_{G}m'_{G}}{d^{2}}}$. Ako je ubrzanje $a$ (i brzina) tela koje je u slobodnom padu nezavisno od inercione mase (kao što je pokazao Galilejev eksperiment), onda za telo važi $m=m_{G}$, dakle gravitaciona masa je jednaka inercionoj masi, što ne zavisi od vrste i sastava tela. Njutn je testirao ovu teoriju na mnogo primera i nije joj našao izuzetak.

Ako zanemarimo ostale uticaje i pretpostavimo da sila deluje trenutno, bez kašnjenja, gravitacionu sila između dva tačkasta tela može se objasniti na sledeći način:

$F=G\cdot {\frac {m_{G}m'_{G}}{d^{2}}}$, gde je $G$ konstanta pod imenom gravitaciona konstanta.

Odavde dobijamo i konačni zapis Univerzalnog zakona gravitacije u skalarnom obliku:

$F_{12}=G\cdot {\frac {m_{1}m_{2}}{d^{2}}}$

I u vektorskom obliku:

${\vec {F}}_{12}=-G\cdot {\frac {m_{1}m_{2}}{d^{2}}}{\vec {u}}_{12}$

Primer

Naći privlačnu silu gravitacije između planete Zemlje i Sunca i njen intenzitet.

Poznate vrednosti su:

• gravitaciona konstanta: $G=6.67\cdot 10^{-11}{\frac {N\cdot m^{2}}{kg^{2}}}$
• udaljenost Zemlje od Sunca $r=1.5\cdot 10^{11}m$
• masa Sunca $m_{1}=1.99\cdot 10^{30}kg$
• masa Zemlje $m_{2}=5.98\cdot 10^{24}kg$

Univerzalni zakon gravitacije glasi:

${\vec {F}}=-G\cdot {\frac {m_{1}m_{2}}{d^{2}}}{\vec {u}},$

gde je ${\vec {u}}$ jedinični vektor od tela 1 ka telu 2.

Na osnovu gorenavedenog, dobijamo da je tražena sila:

${\vec {F}}=-{\frac {6.67\cdot 10^{-11}Nm^{2}\cdot 1.99\cdot 10^{30}kg\cdot 5.98\cdot 10^{24}kg}{kg^{2}\cdot (1.5\cdot 10^{11}m)^{2}}}=-3.52\cdot 10^{22}N\cdot {\vec {u}},$

a njen intenzitet:

$F=3.52\cdot 10^{22}N.$

Znak minus (-) u jednačini sile pokazuje da je sila između Zemlje i Sunca privlačna sila.

Opštost Univerzalnog zakona gravitacije

Slika prikazuje 3 Keplerova zakona sa dve planetarne putanje:
(1) Putanje planeta su elipse, sa žarištima ƒ₁ i ƒ₂ za prvu planetu i ƒ₁ i ƒ₃ za drugu planetu. Sunce je smešteno u žarištu ƒ₁.
(2) Dva zasenčena područja A₁ i A₂ imaju jednake površine i vreme za planetu 1 da prekrije područje A₁ je jednako da prekrije područje A₂.
(3) Ukupna ophodna vremena planeta 1 i planeta 2 imaju odnos t₁^3/2 : t₂^3/2.

Koliko je Njutnov zakon gravitacije opštiji u odnosu na zakone koji su do tada postojali i koji su bili i eksperimentalno potvrđeni, pokazuje činjenica da se svi ti zakoni mogu dokazati iz njega i da oni predstavljaju samo neke od specijalnih slučajeva tog zakona.

Keplerovi zakoni

Glavni članak: Keplerovi zakoni

Pomoću Univerzalnog zakona gravitacije, mogu se dokazati i svi Keplerovi zakoni i uočavaju se greške u Trećem Keplerovom zakonu.

Galilejev zakon

Glavni članak: Galilejev zakon

Njutnov zakon gravitacije može da iskaže Galilejev zakon. Ako se sa $d$ označi poluprečnik zemlje, a $m_{T}=$ je masa Zemlje, dobija se da je $g=G\cdot {\frac {m_{T}}{d^{2}}}=9,81$ m·s⁻².

Primena

Ponašanje satelita i projektila, pošto podležu Univerzalnom zakonu gravitacije

Kao i svaka teorija, i Univerzalni zakon gravitacije je od hipoteze eksperimentalno potvrđen.

Jedno od otkrića, kojem je osnovnu podlogu dao upravo Univerzalni zakon gravitacije, je otkriće da je moguće u vazduh podignuti, tj. poslati na nebo i predmete koji su teži od vazduha.

Zakon gravitacije i kretanja tela

Uobičajeno je da se slobodni pad uzima kao primer uniformnog ubrzanog kretanja (kretanja sa stalnim ubrzanjem). Pritom se pretpostavlja da nema otpora vazduha ili trenja.

Kružno kretanje je sastavljeno od dve komponente, od kretanja stalnom brzinom po pravcu i od uniformno ubrzanog kretanja sa smerom prema središtu kruženja.

Vizuelni primer kretanja veštačkih satelita GPS-a zajedno sa Zemljinom rotacijom.

Za Zemlju (M = 6 ∙10²⁴ kg) brzina kruženja ili orbitalna brzina na samoj površini (r = 6 378 km) iznosila bi 7 910 m/s ili 7,91 km/s. Ta se brzina zove i prvom kosmičkom brzinom.

Njutnova zamišljena topovska kugla: ukoliko bi top na nekoj uzvisini ispalio kuglu s brzinom manjom od brzine kruženja (v_k = 7.9 km/s) ona bi imala putanju A ili B i pala bi na Zemlju; ukoliko bi kugla išla brzinom kruženja ona bi imala kružnu putanju C i kretala bi se stalnom brzinom; ukoliko bi kugla krenula brzinom većom od brzine kruženja ona bi putovala po elipsi D; ukoliko bi kugla krenula brzinom većom od brzine oslobađanja (v_o = 11,2 km/s) ona bi putovala po hiperboli E i napustila bi Zemlju.

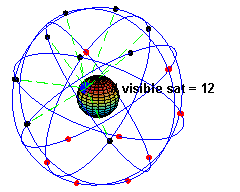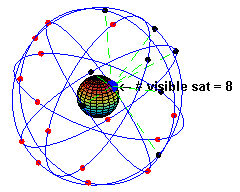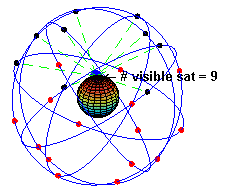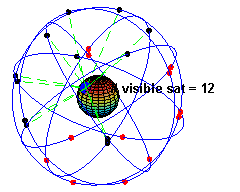
Pojave u prirodi tumače se međudelovanjima (interakcijama). Njutnov zakon gravitacije je matematički opis gravitacione sile ili gravitacione interakcije - sile kojom se uzajamno privlače dve mase. Dok su Keplerovi zakoni opisivali način kretanja planeta, Njutnov zakon gravitacije je pomogao da se rastumači zašto se planete kreću baš tako kako se kreću. Njutn je zakon izveo na temelju praktičnog iskustva i teorijskih razmatranja tadašnje fizike i astronomije, uključivši Keplerove zakone. Obratno, matematičkim se putem iz Njutnovog zakona gravitacije mogu izvesti Keplerovi zakoni. Ali ne samo to. U prirodi ima kretanja koja su mnogo složenija od kretanjaa pojedine planete oko Sunca. Već je kretanje planetoida i kometa složenije od kretanja planeta. Isto je tako složenije kretanje mnoštva zvezda u jednom skupu zvezda, ili zvezda jedne galaksije, a sva su ona uslovljena Njutnovom silom. Stoga je Njutnov zakon gravitacije mnogo opštiji i i važi u celom svemiru.

Svojstva te gravitacione sile su sledeća. Ona je uzajamna, privlačna i centralna sila. Uzajamna je zato što jednakom silom kojom telo mase M privlači masu m, privlači i telo mase m masu M. Centralna je zato što je usmerena od jedne mase prema drugoj. Nadalje, sila je srazmerna masi svakog tela posebno, a njena veličina opada obrnuto srazmerno s kvadratom udaljenosti. Ako se razmak tela udvostruči, sila se smanji četiri puta; ako se utrostruči, smanji se devet puta.

Konstanta G (univerzalna gravitaciona konstanta) je konstanta proporcionalnosti i prema merenjima iznosi oko 6,67428 ∙ 10⁻¹¹ N m² kg⁻². Tela obično se predstavljaju malim kuglama. Zakon treba primenjivati na tačkasta tela (tela sažeta u materijalne tačke). Ako tela nisu tačkasta, već proširena, tada je ukupna sila između njih jednaka zbiru svih sila između svake dve materijalne tačke. Stoga gravitaciono polje oko stvarnog (realnog) tela može biti veoma složeno.

Slobodni pad

Gravitaciona sila je uzrok kretanja i promjena stanja kretanja. U polju gravitacije tela se kreću ubrzano. Zato se u ubrzanju tela odražavaju svojstva gravitacione sile. Ubrzanje ili akceleracija nekog malog tela mase m koje se nalazi u polju sfernog tela mase M, prema Drugom Njutnovom zakonu kretanja ili temeljnom zakonu kretanja glasi:

$F=m\cdot g$

Konstanta proporcionalnosti između sile i ubrzanja je masa ubrzavanog tela. Na telo mase m deluje Njutnova sila, jer se ono nalazi u gravitacionom polju koje okružuje masu M. Izjednačavanjem gornjih izraza dobija se:

$g=G{\frac {Mm}{r^{2}}}\$

To je ubrzanje (akceleracija) tela mase m u gravitacionom polju mase M, na rastojanju r od mase M. Ubrzanje ili akceleracija ima ujedno dimenziju jačine gravitacionog polja; jačina gravitacionog polja je odnos gravitacione sile i ubrzavane mase. Uobičajeno je da se slobodni pad (ili kretanje kosinom) uzima kao primer uniformnog ubrzanog kretanja (kretanja sa stalnim ubrzanjem). Pritom se pretpostavlja da nema otpora vazduha ili trenja. Gornji matematički izraz treba uzimati s oprezom. Ako i nema otpora, telo će se kretati stalnim ubrzanjem samo na veoma malom delu puta, na onom delu na kojemu se r vrlo malo menja. Prema tome, slobodni pad se može uzimati kao primer uniformnog ubrzanog kretanja jedino kod malih visina pada. Ako je ubrzanje stalno, put s prevaljen u smeru ubrzanja za vreme t jednak je:

$s={g \over 2}\cdot t^{2}$

Kruženje satelita

Isak Njutn je shvatio da je kružno kretanje sastavljeno od dve komponente, od kretanja stalnom brzinom po pravcu i od uniformno ubrzanog kretanja sa smerom prema središtu kruženja. Kad ne bi bilo privlačenja, telo bi uniformnom brzinom v_k odmicalo po pravcu i za vreme t prešlo put v_k∙t. Isto tako, zbog gravitacionog privlačenja, telo pada prema centru i u tom padu, u vreme t, prevali put gt²/2. Ako telo ipak ostaje na kružnici, mora biti da se ono tokom vremena t za toliko odmakne od kružnice za koliko ujedno i padne na kružnicu. Taj proces prisutan je na svakom mestu kružnice, na svakom ma kako malom odsečku puta. Ako bi brzina kretanja v bila manja od brzine kruženja v_k, to telo bi zbog slobodnog pada prišlo centru Zemlje više nego što bi se u jednolikom kretanju po pravcu od nje odmaknulo, pa bi tako prelazilo s kružnice većeg poluprečnika na kružnicu manjeg poluprečnika, te bi u spirali napokon palo na Zemlju.

Prisili li se neko telo da se na vrtešci kreće brzinom v, tada ono u smeru prema centru ima ubrzanje g (centripetalno ubrzanje). Između brzine kretanja v po kružnoj stazi poluprečnika r i centripetalne akceleracije g postoji veza:

$g={\frac {v^{2}}{r}}$

Kreće li se telo po kružnici i pojača li se centripetalna sila, porašće i ubrzanje i brzina. Ako je sila privlačenja gravitaciona, i u centru kretanja se nalazi masa M, tada je centripetalno ubrzanje potpuno određeno i jednako izrazu:

$g=G{\frac {M}{r^{2}}}\$

Tim uslovom se za dati poluprečnik staze od svih mogućih centripetalnih ubrzanja odabira samo jedno ubrzanje (akceleracija), a njoj odgovara samo jedna, potpuno određena brzina. Izjednačavanjem gornja dva izraza, dobija se:

$v=v_{k}={\sqrt {\frac {GM}{r}}}$

Za Zemlju (M = 6 ∙10²⁴ kg) brzina kruženja ili orbitalna brzina na samoj površini (r = 6 378 km) iznosila bi 7 910 m/s ili 7,91 km/s. Ta se brzina zove i prvom kosmičkom brzinom. Na svakom drugom nivou iznad površine Zemlje brzina kruženja ima drugu vrednost.

Oslobađanje satelita

Kada se brzina satelita poveća iznad brzine kruženja v_k dolazi do izduženja staze (putanje). Kružnica prelazi u elipsu, a elipsa malog ekscentriciteta prelazi u elipsu većeg ekscentriciteta. Kada staza postane parabola, telo će napustiti Zemljinu blizinu i slobodno odletjeti u međuplanetarni prostor. To je brzinu oslobađanja v_o ili druga kosmička brzina. Tela mogu biti međusobno vezana, ili slobodna. Telo je vezano i čini jedan fizički sistem sa Zemljom kada leži na njoj ili se kreće oko nje zatvorenom putanjom. Uopšteno, telo ima i kinetičku energiju i gravitacionu potencijalnu energiju (energiju položaja u gravitacionom polju). Potencijalna energija E_p mase m u okolini mase M jednaka je:

$E_{p}={\frac {-GMm}{r}}$

Dogovorom je potencijalnoj energiji dodeljen negativan predznak. Na manjoj udaljenosti р potencijalna energija je negativnija nego na većoj udaljenosti. S povećanjem razmaka potencijalna energija poprima manje negativnu vrednost, a na beskonačnoj udaljenosti iznos joj padne na nulu. Zapravo, relativno najveću vrednost ima potencijalna energija na najvećoj udaljenosti; to je smisao negativnog predznaka. U strogom značenju telo je slobodno kada se nalazi na neizmernoj udaljenosti od Zemlje. S obzirom na to da Zemlja nije sama u svemiru, već je svemirsko gravitaciono polje složeno od mnogih pojedinačnih, telo će se uvek nalaziti pod njihovim uticajem. Zato je i pitanje slobode više praktičko pitanje: na velikim udaljenostima od Zemlje telo se nalazi u slobodnom stanju. Odnos gravitacione potencijalne energije i mase m, dakle izraz - GM/r, zove gravitacioni potencijal.

Može se zamisliti postupak oslobađanja tela u slučaju kada je telo na početku mirovalo na Zemlji, a na kraju mirovalo na praktično beskonačnoj udaljenosti od Zemlje. Kako je kinetička energija u takvom slučaju i na početku i na kraju postupka jednaka nuli, to će telo morati premostiti razliku potencijalne energije E_p koja postoji između površine Zemlje i beskonačne udaljenosti. Promena energije jednaka je konačnoj vrednosti manje početne vrednosti. Budući da se energija ne može ni stvoriti niti izgubiti (zakon očuvanja energije), treba je preuzeti iz kinetičke energije E_k, telo treba odaslati sa Zemlje s nekom početnom brzinom v_o:

$(E_{p}+E_{k})_{Z}=(E_{p}+E_{k})_{s}\,$

${\frac {1}{2}}mv_{o}^{2}+{\frac {-GMm}{r}}=0+0$

Telo se mora krenuti sa brzinom oslobađanja v_o:

$v_{o}={\sqrt {\frac {2GM}{r}}}$

Postupak se može odvijati i u suprotnom smeru. Pri slobodnom padu od beskonačnosti do daljine r razlika potencijalne energije prelazi u kinetičku, i brzina v_o koju telo ima zavisi od udaljenosti r od centra privlačenja mase M. To znači da bi telo u slobodnom padu palo do nekog položaja r s istom onom brzinom s kojom se s tog položaja u gravitacionom polju mora osloboditi. Brzina oslobađanja sa Zemlje iznosi 11,2 km/s i naziva se još drugom kosmičkom brzinom. Ako se želi da se telo koje već kruži oko mase M oslobodi, trebaće mu do brzine oslobađanja dodeliti manju energiju nego kad je ležalo na Zemlje. Brzinu tela treba povećati od v_k do v_o, zapravo kinetičkoj energiji treba dodati iznos G M m / 2 r. Telu treba dovesti još toliko kinetičke energije koliko kinetičke energije već ima. Na takav se način postupa s svemirskim letelicama koje se otpremaju na planete. One se najpre lansiraju u putanju oko Zemlje, gde je bezvazdušni prostor, a onda se u odabranom trenutku ponovo pale raketni motori, raketa postiže brzinu oslobađanja i usmerava letilicu prema cilju.

Kretanje veštačkih satelita

Veštački sateliti se lansiraju u putanje koje imaju različite ekscentricitete. Brzina kojom se kreću zavisi od položaja na putanji. Na većim udaljenostima od Zemlje brzina kruženja v_k manja je od 7,9 km/s. Na slici je nekoliko oblika putanje satelita koji prolaze tačkom koja je na nekoj visini od površine Zemlje. Tačka najbliža Zemlji na toj putanji zove se perigej, a tačka najveće udaljenosti apogej. Putanja C je kružnica i satelit se kreće sa stalnom brzinom, s brzinom kruženja za tu daljinu. Staza D je eliptična. S približavanjem perigeju satelit postiže najveću brzinu, koja je veća od brzine kruženja na tom mestu; da je jednaka brzini kruženja, satelit bi se kretao kružnicom. Eliptičnu putanju D ima veštački satelit koji se kreće brzinom većom od brzine kruženja, a manjom od brzine oslobađanja.

Po nekim osobinama kretanje veštačkih satelita razlikuje se od kretanja prirodnih satelita. Najveća je razlika u tome što je masa veštačkih satelita sasvim zanemariva prema masi Zemlje. Osim Zemlje, na putanju satelita utiču i Mesec i Sunce. Zato se satelit kreće u složenom gravitacionom polju. Ni sama Zemlja nema jednostavno gravitaciono polje kakvo ima tačkasta masa, jer je spljoštena na polovima, odnosno ispupčena na ekvatoru, a osim toga, unutar već složenog oblika, materija nije jednoliko raspoređena. Mase su različito raspoređene u području mora i kopna. Veću gustinu imaju slojevi tla koji se nalaze ispod okeana, manju slojevi ispod kopna. Putanja satelita stalno se poremećuje, neprestano se menjaju orbitalni elementi satelita, te se ta poremećenja upravo mogu iskoristiti da bi se ocenio oblik Zemlje i raspored masa. Podaci dobijeni nakon analize kretanja satelita nadopunjuju podatke dobijene neposrednim geodetskim premerima Zemlje i gravimetrijskim merenjima (merenjima ubrzanja sile teže).

Drugi uzrok koji dovodi do stalne promene putanje Zemljinog veštačkog satelita je otpor Zemljine atmosfere. Atmosfera postoji i na vrlo velikim visinama, makar i retka, pa se njen uticaj oseti nakon nekog vremena. Jasno je da je uticaj jači u nižim delovima putanje, dok je satelit blizu perigeja. Satelit gubi energiju, apogej se približava Zemlji i putanje se zaobljuje. Elipsa prelazi u kružnicu, a čitava se putanja smanjuje i približava Zemlji. Satelit tone sve dublje i spiralno ulazi u gušće delove atmosfere gde izgara, a katkada pokoji njegov deo dospeva i do tla.

Vidi još

• Gravitacija
• Njutnovi zakoni - osnovni zakoni klasične mehanike
• Keplerovi zakoni
• Galilejev zakon
• Isak Njutn

Спољашње везе

• Feather & Hammer Drop on Moon на сајту YouTube
• Newton‘s Law of Universal Gravitation Javascript calculator