Електрични потенцијал
| Електрични потенцијал | |
|---|---|
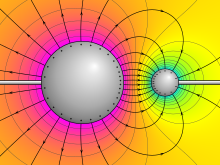 Електрични потенцијал око две супротно наелектрисане проводне сфере. Љубичаста представља највећи потенцијал, жута нула, а цијан најмањи потенцијал. Приказане су електричне линије поља које напуштају управно на површину сваке сфере. | |
Уобичајени симболи | V, φ |
| СИ јединица | волт |
Друге јединице | Статволт |
| У СИ базним јединицама | V = kg⋅m2⋅s−3⋅A−1 |
| СИ димензија | M L2 T−3 I−1 |
| Екстензивне? | да |
| Електромагнетизам |
|---|
 |
Електрични потенцијал или електрични скаларни потенцијал је потенцијал који одговара електричном пољу.[1][2] Електрични потенцијал је особина која карактерише сваку тачку у простору, а њена квантитативна вредност једнака је количнику потенцијалне електричне енергије по јединици наелектрисања које се налази се у статичком (временски непроменљивом) електричном пољу. Електрични потенцијал је скаларна величина, уобичајено изражена у волтима. У електромагнетизму, електрични потенцијал се уводи као скаларна функција чији је негативни градијент једнак вектору електричног поља: .
Назив електрични скаларни потенцијал се користи у електродинамици када електрично поље у ком се посматрано наелектрисање налази није статичко, већ је временски променљиво. Реч скаларни у називу наглашава да је потенцијал описан једном компонентом, за разлику од магнетног векторског потенцијала за чије описивање је потребно три компоненте.[3] Електрични потенцијал и вектор магнетног потенцијала формирају четворовектор потенцијала, тако да су ова два потенцијала спрегнути, а њихове трансформације дефинисане су Лоренцовим трансформацијама.[4]
Електрично поље[уреди | уреди извор]
Познато је да неки предмети могу имати електрични набој односно наелектрисање. Електрично поље врши померање наелектрисаних честица, убрзавајући их у смеру вектора електричног поља, односно у смеру или насупрот смеру вектора електричног поља, у зависности од врсте наелектрисања.[5][2] Уколико је наелектрисана честица наелектрисана позитивним наелектрисањем, сила деловања и убрзања те честице ће бити у смеру са електричним пољем, а вредност силе која делује, одређена је величином наелектрисања честице и вредношћу електричног поља.
Електрична сила и електрична потенцијална енергија су у директном односу. Како се честица креће у смеру у којем га сила убрзава, њена потенцијална енергија се смањује. Такав однос имају и друге врсте сила и њима одговарајућих потенцијалних енергија. На пример, како објекат пада услед привлачења гравитационе силе, његова гравитациона потенцијална енергија се смањује.
Потенцијал електричног поља се назива електрични потенцијал и најчешће се означава са , или V. Разлика електричног потенцијала између две тачке у простору, назива се напон.
Формална дефиниција[уреди | уреди извор]
Електрични скаларни потенцијал се уводи преко електричног поља . Електрични скаларни потенцијал је скаларна функција чији је негативни градијент једнак вектору електричног поља:
Како је ротор стационарног електричног поља једнак нули, , дат линијски интеграл не зависи од специфичне путање C, већ само од крајњих тачака и одавде се добија да је електрични потенцијал једнак:
где је C путања по којој се интеграли, а која повезује извор електричног поља и тачку за коју се потенцијал израчунава.
Ако је позната потенцијална електрична енергије честице q, потенцијал се може изразити и као:
Из Гаусове теореме која у интегралном облику тврди да је флукс електростатичког поља у вакууму кроз било коју затворену површину једнак количнику укупног наелектрисања које се налази у запремини обухваћеном том површи и диелектричне константе вакуума. Одавде следи да потенцијал задовољава Поасонову једначину:[6][7]
где је ρ укупна густина наелектрисања која обухвата и слободна и везана наелектрисања.
Увод у електромагнетизам[уреди | уреди извор]
У случају када ротор електричног поља није нула, , тј. ако поље није стационарно, електрични потенцијал се не може непосредно изразити као:
јер тада електрично поље није више конзервативно и интеграција зависи од конкретне путање. Тада се скаларни електрични потенцијал мора дефинисати заједно са магнетним векторским потенцијалом .
где је густина флукса магнетског поља (такође познат као магнетна индукција или магнетско поље). Увек се може пронаћи такво зато што (одсуство магнетног монопола). Вредност је конзервативно поље одређено Фарадејевим законом и може се писати:
где је φ скаларни потенцијал описан конзервативним пољем .
Електростатички потенцијал, једноставно је посебан случај ове дефиниције где је временски непроменљива вредност. Са друге стране, за временски променљива поља важи следеће .
Обратите пажњу да ова дефиниција φ зависи од нормирања потенцијалне функције за вектор потенцијала (градијент било којег скаларног поља може бити додат без мењања ). Један начин је да #Кулонов калибрациони услов (за потенцијал) Нормирање потенцијалне функције, у којем ћемо изабрати услов да је . У овом случају, добијамо , где је ρ густина наелектрисања. Други начин је Лоренцов калибрациони услов, у којем усвајамо да би задовољили .
Посебни случајеви и примери израчунавања[уреди | уреди извор]
Електрични потенцијал у тачки у константном електричном пољу може се представити:
Електрични потенцијал око тачкастог наелектрисања q, на удаљености r од наелектрисања, рачуна се:
Укупан потенцијал низа пунктуалних наелектрисања једнак је суми појединачних потенцијала свих наелектрисања. Ова чињеница поједностављује прорачун у великој мери, због тога што је сабирање потенцијала (скаларно) поља много једноставније него сабирање вектора електричног поља.
Електрични потенцијал настао од тродимензионалног сферно симетричног Гаусовог наелектрисања густине се рачуна следећим изразом:
где је q количина наелектрисања, добијен је решавањем Поасонове једначине:
решење је преко:
где је erf(x) функција грешке. Ово решење се може проверити опрезном ручном евалуацијом . Обратите пажњу, да за r много веће од σ, erf(x) потенцијал постаје по вредности ближи потенцијалу пунктуалног наелектрисања .
Примена у електроници[уреди | уреди извор]
Електрични потенцијал, уобичајено мерен у волтима, обезбеђује једноставан начин анализирања електричних кола без претходног познавања облика кола или поља у њима.
Електрични потенцијал обезбеђује једноставан начин анализе електричних кола уз помоћ Кирхофових закона,[8][9][10] без потпуног решавања Максвелових једначина за статичка електрична поља.[11][12]
Јединице[уреди | уреди извор]
СИ јединица за електрични потенцијал је волт (у част Алесандро Волта), и у толико широкој употреби је да су термини напон и електрични потенцијал постали синоними. Старије јединице су ретке. Варијанте јединице електричног потенцијала су статволт (= 299.792 458 V) и абволт који је ≡ 1×10−8 V.
Референце[уреди | уреди извор]
- ^ Roche, John (2016). „Introducing electric fields”. Physics Education. 51 (5): 055005. Bibcode:2016PhyEd..51e5005R. S2CID 125014664. doi:10.1088/0031-9120/51/5/055005.
- ^ а б Purcell, Edward M.; Morin, David J. (2013). Electricity and Magnetism (3rd изд.). New York: Cambridge University Press. стр. 16—20. ISBN 978-1-107-01402-2.
- ^ Griffiths, David J. (1999). Introduction to Electrodynamics. Pearson Prentice Hall. стр. 416–417. ISBN 978-81-203-1601-0.
- ^ Goldstein, Herbert (јун 1959). Classical Mechanics. United States: Addison-Wesley. стр. 383. ISBN 0201025108.
- ^ Feynman, Richard (1970). The Feynman Lectures on Physics Vol II. Addison Wesley Longman. стр. 1—3,1—4. ISBN 978-0-201-02115-8.
- ^ Jackson, Julia A.; Mehl, James P.; Neuendorf, Klaus K. E., ур. (2005), Glossary of Geology, American Geological Institute, Springer, стр. 503, ISBN 9780922152766
- ^ Poisson (1823). „Mémoire sur la théorie du magnétisme en mouvement” [Memoir on the theory of magnetism in motion]. Mémoires de l'Académie Royale des Sciences de l'Institut de France (на језику: француски). 6: 441—570.
- ^ Oldham, Kalil T. Swain (2008). The doctrine of description: Gustav Kirchhoff, classical physics, and the "purpose of all science" in 19th-century Germany (Ph. D.). University of California, Berkeley. стр. 52. Docket 3331743.
- ^ Oldham, Kalil T. Swain (2008). The doctrine of description: Gustav Kirchhoff, classical physics, and the "purpose of all science" in 19th-century Germany (Ph. D.). University of California, Berkeley. стр. 52. Docket 3331743.
- ^ Griffiths, David J (1999). Introduction to electrodynamics (Third изд.). Prentice Hall. ISBN 978-0-13-805326-0.
- ^ Hampshire, Damian P. (29. 10. 2018). „A derivation of Maxwell's equations using the Heaviside notation”. Philosophical Transactions of the Royal Society Research Article. Theme issue Celebrating 125 years of Oliver Heaviside's ‘Electromagnetic Theory’ compiled and edited by Christopher Donaghy-Spargo and Alex Yakovlev PubMed:30373937. Royal Society. 376 (2134). Bibcode:2018RSPTA.37670447H. ISSN 1364-503X. PMC 6232579
 . PMID 30373937. arXiv:1510.04309
. PMID 30373937. arXiv:1510.04309  . doi:10.1098/rsta.2017.0447.
. doi:10.1098/rsta.2017.0447.
- ^ „The NIST Reference on Constants, Units, and Uncertainty”.
Литература[уреди | уреди извор]
- Politzer, Peter; Truhlar, Donald G. (1981). Chemical Applications of Atomic and Molecular Electrostatic Potentials: Reactivity, Structure, Scattering, and Energetics of Organic, Inorganic, and Biological Systems. Boston, MA: Springer US. ISBN 978-1-4757-9634-6.
- Sen, Kalidas; Murray, Jane S. (1996). Molecular Electrostatic Potentials: Concepts and Applications. Amsterdam: Elsevier. ISBN 978-0-444-82353-3.
- Griffiths, David J. (1999). Introduction to Electrodynamics
 (3rd. изд.). Prentice Hall. ISBN 0-13-805326-X.
(3rd. изд.). Prentice Hall. ISBN 0-13-805326-X. - Jackson, John David (1999). Classical Electrodynamics (3rd. изд.). USA: John Wiley & Sons, Inc. ISBN 978-0-471-30932-1.
- Wangsness, Roald K. (1986). Electromagnetic Fields (2nd., Revised, illustrated изд.). Wiley. ISBN 978-0-471-81186-2.
- Sears, Francis; et al. (1982), University Physics (6th изд.), Addison Wesley, ISBN 0-201-07199-1
- Umashankar, Korada (1989), Introduction to Engineering Electromagnetic Fields, World Scientific, стр. 77—79, ISBN 9971-5-0921-0
- Morely & Hughes (1970), Principles of Electricity (5th изд.), стр. 73, ISBN 0-582-42629-4
- Tou, Stephen (2011). Visualization of Fields and Applications in Engineering. John Wiley and Sons. стр. 64. ISBN 9780470978467.
- Griffiths, David J. (1999). Introduction to electrodynamics (3rd изд.). Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-805326-X. OCLC 40251748.
- Browne, Michael (2011). Physics for Engineering and Science (2nd изд.). McGraw-Hill, Schaum, New York. ISBN 978-0-07-161399-6.
- Rindler, Wolfgang (1991). Introduction to Special Relativity (2nd)
 . Oxford: Oxford University Press. ISBN 0-19-853952-5.
. Oxford: Oxford University Press. ISBN 0-19-853952-5. - Jackson, J D (1999). Classical Electrodynamics (3rd). New York: Wiley. ISBN 0-471-30932-X.
- Larmor Joseph (1897). „On a dynamical theory of the electric and luminiferous medium. Part 3, Relations with material media”. Phil. Trans. R. Soc. 190: 205—300.
- Lorentz Hendrik (1899). „Simplified theory of electrical and optical phenomena in moving systems”. Proc. Acad. Science Amsterdam. I: 427—443.
- Lorentz Hendrik (1904). „Electromagnetic phenomena in a system moving with any velocity less than that of light”. Proc. Acad. Science Amsterdam. IV: 669—678.
- Henri Poincaré (1900) "La théorie de Lorentz et le Principe de Réaction", Archives Néerlandaises, V, 253–278.
- Henri Poincaré (1902) "La Science et l'Hypothèse".
- Henri Poincaré (1905) "Sur la dynamique de l'électron", Comptes Rendus de l'Académie des Sciences, 140, 1504–1508.
- Catt, Walton and Davidson. "The History of Displacement Current" Архивирано 2008-05-06 на сајту Wayback Machine. Wireless World, March 1979.
Спољашње везе[уреди | уреди извор]
- Introduction to Electric Potential Концептуални увод
- Electric field in "Electricity and Magnetism", R Nave – Hyperphysics, Georgia State University
- Frank Wolfs's lectures at University of Rochester, chapters 23 and 24
- Fields Архивирано на сајту Wayback Machine (27. мај 2010) – a chapter from an online textbook

































