Електростатика
| Електромагнетизам |
|---|
 |

Електростатика је грана физике која се бави појавама и својствима стационарних или спорокрећућих наелектрисања која немају убрзање.
Од античких времена је познато да одређени материјали као што су ћилибари привлаче лагане честице након трљања. Грчка реч за ћилибар, ήλεκτρον grč. electron, је корен речи 'електрицитет'. Електростатичке појаве потичу од силе која се јавља између наелектрисања. Те силе су описане Кулоновим законом. Иако електростатички индуковане силе изгледају прилично слабе, електростатичке силе између електрона и протон протона који сачињавају атом водоника су око 36 пута јаче од гравитационих сила између њих.
Постоји мноштво примера за електростатичке појаве, од једноставних као што је привлачење пластичне кухињске фолије за вашу руку након што је одмотате из паковања, до наизглед спонтаних експлозија силоса са житом, до оштећења електронских компоненти током производње и функционисања фотокопир машине. Електростатика је повезана са нагомилавањем наелектрисања на површини објеката због додира са другим површинама. Иако се размена наелектрисања дешава сваки пут када се неке две површине додирну и одвоје, ефекат размене наелектрисања се углавном једино примети када бар једна од површина има велики отпор према кретању наелектрисања. То се дешава зато што наелектрисања која прелазе са или на високо отпорну површину су више или мање заробљена на њој довољно дуго да би ефекти наелектрисања могли да се посматрају. Ова наелектрисања остају на објекту док не пређу ка земљи или се брзо неутралишу електростатичким пражњењем. Познати ефекат електростатичког удара настаје неутрализацијом накупљеног наелектрисања у телу контактом са непроводним површинама.
Кулонов закон[уреди | уреди извор]
Кулонов закон за интензитет електростатичке силе (у њутнима) између два тачкаста наелектрисања и (у кулонима). Погодно је означити једно од ових наелектрисања, , као тестно наелектрисање, и назвати наелектрисањем извора. Како се теорија буде проширивала, додаће се још извора наелектрисања. Ако је удаљеност (у метрима) између два наелектрисања, онда је сила:
где је ε0 пермитивност вакуума[1]
Интернационалне СИ јединице ε0 су еквивалентне A2s4 kg−1m−3 or C2N−1m−2 или F m−1. Кулонова константа је:
Коришћење ε0 уместо k0 у изражавању Кулоновог закона је повезано са чињеницом да је сила инверзно пропорционална површини лопте са полупречником једнаким удаљености између два наелектрисања.
Један протон има наелектрисање e, а један електрон има наелектрисање −e, где је,
Ове физичка константа физичке константе (ε0, k0, e) су тренутно дефинисане тако да ε0 и k0 су егзактно дефинисане, а e је мера количине.
Електрично поље[уреди | уреди извор]
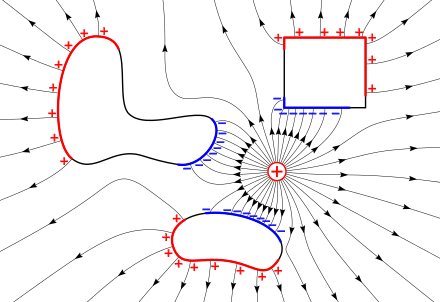
Линије електричног поља су погодне за визуелно представљање електричног поља. Линије поља имају почетак на позитивном наелектрисању и имају крај на негативном наелектрисању у било којој тачки. Електрично поље, , (у јединицама волти по метру) је векторско поље које може да се дефинише било где, осим на месту где се налазе тачкаста наелектрисања (где тежи бесконачности). Погодно је поставити хипотетичко тестно наелектрисање у тачки где се не налазе друга наелектрисања. По Кулоновом закону, ово тестно наелектрисање ће осетити силу која може да се искористи за дефинисање електричног поља на следећи начин:
(Погледати Лоренцове једначине уколико наелектрисање није стационарно)
Размотрити скуп честица наелектрисања , која се налазе у тачкама , електрично поље у (звано тачка поља) је:
где је је вектор премештања од тачке поља извора до тачке поља , и је јединични вектор који показује смер поља. За тачкасто наелектрисање које се налази у координатном почетку, интензитет овог електричног поља је и усмерен је од тог наелектрисања. Чињеница да се сила (а самим тим и поље) може израчунати сабирањем свих вредности индивидуалних честица које су извори наелектрисања је пример принципа суперпозиције. Електрично поље које настаје од наелектрисања је задато у [[густина наелектрисања|густини наелектрисања у запремини и може бити израчунато конвертујући ову суму у троструки интеграл:
Гаусов закон[уреди | уреди извор]
Гаусов закон каже да "укупан електрични флукс кроз било коју затворену хипотетичку површину било ког облика унутар електричног поља, пропорционалан укупном наелектрисању унутар те површине“. Математички, Гаусов закон има облик интегралне једначине:
где је елемент запремине. Ако је наелектрисање распоређено по површини или дуж линије, заменити са или . Теорема Дивергенције дозвољава да се Гаусов закон напише у диференцијалном облику:
где је оператор дивергенције.
Поасонове и Лапласове једначине[уреди | уреди извор]
Дефиниција електростатичког потенцијала, комбинована са диференцијалним обликом Гаусовог закона (изнад), даје релацију између потенцијала Φ и густине наелектрисања ρ:
Ова релација је облик Поасонове једначине. У одсуству неупарених наелектрисања, једначина постаје Лапласова једначина:
Електростатичка апроксимација[уреди | уреди извор]
Исправност електростатичке апроксимације се ослања на претпоставку да је електрично поље не ротирајуће:
Из Фарадејевог закона индукције, ова претпоставка подразумева одсуство или скоро потпуно одсуство временски променљивих магнетних поља:
Другим речима, електростатика не захтева одсуство магнетних поља или електричних струја. Тачније, уколико магнетна поља постоје или електричне струје, оне не смеју да се мењају током времена, или у најгорем случају, морају да се мењају у току времена веома полако. У неким проблемима, и електростатика и магнетостатика су потребни за добијање тачних прогноза, али међусобни ефекти могу и даље да се игноришу.
Електростатички потенцијал[уреди | уреди извор]
Пошто је електрично поље не ротирајуће, могуће је изразити електрично поље као градацију скаларне функције,, која се назива електростатичким потенцијалом или познатије напоном. Електрично поље, , је усмерено од области са високим електричним потенцијалом ка областима са малим електричним потенцијалом, математички изражено са
Теорема градијента може да се искористи како би се установило да је електростатички потенцијал мера физичког рада по јединици наелектрисања које је потребно да би се наелектрисање померило из тачке у тачку , изражено интегралом:
Из ових једначина, видимо да је електрични потенцијал константан у било којој области у којој нема електричног поља (као што се дешава унутар проводних објеката).
Електростатичка енергија[уреди | уреди извор]
Потенцијална енергија једне тестне честице, , може да се израчуна из интеграла уложеног рада,. Интеграција се врши из тачке која је бесконачно удаљена, и претпоставља се да се скуп честица са наелектрисањем , већ налази у тачкама . Ова потенцијална енергија (у Џулима) је:
где је раздаљина сваког наелектрисања од тестног наелектрисања , које се налази у тачки , а је електрични потенцијал који би се налазио да тестно наелектрисање није присутно. Ако су присутна само два наелектрисања, потенцијална енергија једнака је . Укупна електрична потенцијална енергија која настаје од присуства скупа од N наелектрисања се израчунава сабирањем потенцијалних енергија сваке честице:
где сума, j = 1 do N, искључује i = j:
Овај електрични потенцијал, је вредност која би се измерила у тачки ако би недостајало наелектрисање . Ова формула очигледно искључује бесконачно велику енергију која би била потребна за сакупљање сваке тачке наелектрисања из облака наелектрисања. Сума наелектрисања може да се конвертује у интеграл над густином наелектрисања користећи следећи рецепт :
- ,
Овај други израз за електростатичку енергију користи чињеницу да је електрично поље негативна градација електричног потенцијала. Ова два интеграла за електрично поље наизглед показују две међусобно искључујуће формуле за густину електростатичке енергије, тј. и ; оне добијају исте вредности за укупну електростатичку енергију, само ако се изврши интеграција обе једначине кроз цео простор.
Електростатички притисак[уреди | уреди извор]
На електричном проводнику, површинска наелектрисања ће осећати силу у присуству електричног поља. Ова сила је усредњена вредност дисконтинуалног електричног поља на површинско наелектрисање. Ова усредњена вредност у односу на поље присутно одмах око површине даје:
- ,
Овај притисак има тенденцију да увлачи проводник у поље, независно од знака површинског наелектрисања.
Трибоелектрична серија[уреди | уреди извор]
Трибоелектрични ефекат је врста електрификације контакта у којој одређени материјал постаје наелектрисан када додирне други контакт од другог материјала, па се затим удаљи од њега. Један од материјала добија позитивно наелектрисање, а други једнако негативно наелектрисање. Знак и јачина наелектрисања који настају се разликује од врсте материјала, површинске грубоће, температуре, оптерећења, и других особина. Ћилибар на пример може да прими наелектрисање трљањем са материјалом као што је вуна. Ову особину је први пут забележио Талес из Милета, и представља први електрични феномен који је човек истражио. Други примери материјала који могу да добију значајно наелектрисање трљањем су стакло које се трља о свилу, и тврда гума која се трља о крзно.
Електростатички генератори[уреди | уреди извор]
Присуство дисбаланса површинских наелектрисања значи да ће тела показати привлачне или одбојне силе. Овај дисбаланс површинских наелектрисања који доводи до статичког електрицитета, може да настане додиривањем две различите површине и њиховим одвајањем због феномена електрификације контаката и трибоелектричног ефекта. Трљање два непроводна тела ствара велику количину статичког наелектрисања. Оно није само резултат трења; две непроводне површине могу да се наелектришу само постављањем једне на другу. Пошто већина површина има грубу површину, потребно је да прође више времена за наелектрисање контактом него трљањем. Трљање објеката међусобно повећава величину контактне површине између њих. Углавном изолатори, супстанце које не проводе електрицитет, су добре за генерисање и задржавање површинског наелектрисања. Неки примери оваквих материјала су гума, пластика и стакло. Проводници се ретко наелектришу сем у случајевима када је нпр. метална површина ударена чврстим или течним изолатором. Наелектрисање које се пребацује преко електрификације контакта се чува на површинама објеката. Електростатички генератори су уређаји који производе веома велики напон са веома малом струјом и користе се у учионицама за демонстрацију физике а њихов принцип рада се ослања на претходно описан ефекат.
Приметите да присуство електричних струја не утиче на смањење електростатичких сила или варничења.
Неутрализација наелектрисања[уреди | уреди извор]
Природни електростатички феномени су познати као повремено досадне појаве у сезонама мале влажности ваздуха, али могу бити деструктивни у неким ситуацијама (нпр. у производњи електронике). Када се ради у директном контакту са интегрисаним електронским компонентама (посебно осетљивим МОСФЕТ транзисторима), или у присуству запаљивог гаса, морају се предузети мере опреза да би се спречило скупљање и нагло електростатичко пражњење.
Индукција наелектрисања[уреди | уреди извор]
Индукција наелектрисања се јавља када негативно наелектрисано тело одбија електроне са површине другог тела. Ово ствара област у другом телу које је више позитивно наелектрисано. Привлачна сила се онда јавља између два објекта. Нпр. када се балон трља, балон ће се залепити за зид јер је привлачна сила јавља између две супротно наелектрисане површине (зид добија електрично наелектрисање због индукције наелектрисања, пошто се слободни електрони на површини зида одбијају о негативно наелектрисан балон, стварајући позитивно наелектрисану површину зида, која се због тога привлачи са површином балона). Истражите овај ефекат помоћу симулацијеballoon and static electricity.
Статички електрицитет[уреди | уреди извор]

Пре 1832. године када је Мајкл Фарадеј објавио резултате свог експеримента на тему идентитета електрицитета, физичари су "статички електрицитет" сматрали другачијим у односу на остала наелектрисања. Мајкл Фарадеј је доказао да су електрицитет индукован магнетом, напонски електрицитет из батерије и статички електрицитет једнаки.
Статички електрицитет уобичајено настаје када се два материјала трљају један о други, као вуна на пластици или ђон ципела по тепиху. Процес чини да се електрони извуку из површине једног материјала и преместе на површину другог материјала.
Електростатички удар настаје када површина другог материјала, негативно наелектрисана електронима, додирне позитивно наелектрисан проводник, или супротно.
Статички електрицитет се користи у ксерографији, филтерима ваздуха и неким аутомобилским бојама. Статички електрицитет је накупљено наелектрисање на два тела који су постали одвојени једно од другог. Мале електронске компоненте могу лако да се оштете статичким електрицитетом. Произвођачи компонената користе разне антистатичке уређаје да ово избегну.
Статички електрицитет и хемијска индустрија[уреди | уреди извор]
Када се различити материјали споје и одвоје, може да се акумулира наелектрисање које оставља један материјал позитивно а други негативно наелектрисаним. Мали удар који осетите када пипнете уземљени предмет након ходања по тепиху је пример вишка наелектрисања које се акумулирало у вашем телу од трења између ваших ципела и тепиха. Резултујуће наелектрисање вашег тела може да изазове јако електрично пражњење. Иако експериментисање са статичким електрицитетом може бити забавно, сличне варнице могу да доведу до великих опасности у индустријама које се баве запаљивим материјалима, где мала електрична варница може да запали експлозивну смешу са великим последицама.
Сличан начин наелектрисања настаје када течности мале проводљивости струје теку дуж цеви - процес који се зове електрификација млаза. Течности које имају малу електричну проводљивост (испод 50 пикосименса по метру, где је пикосименс по метру мера електричне проводљивости), називају се акумулатори. Течности које имају проводљивост изнад 50 пикосименса по метру се називају не-акумулатори. Код не-акумулатора, наелектрисања се брзо рекомбинују док се раздвајају и зато наелектрисање које настаје није значајно. У петрохемијској индустрији, 50 пикосименса по метру је минимална вредност електричне проводљивости за адекватно уклањање наелектрисања из течности.
Значајан концепт за изоловање течности је време статичке релаксације. Ово је слично временској константни (tau) унутар РЦ кола. За изолациони материјал, ово представља однос статичке диелектричне константе подељен са електричном проводљивошћу материјала. За угљоводоничне течности, ова мера се понекад апроксимира дељењем броја 18 са електричном проводљивошћу течности. Тако течност која има електричну проводљивост од 1 pS/cm (100 pS/m) ће имати процењену вредност времена релаксације од око 18 секунди. Вишак наелектрисања у течности ће бити скоро комплетно одстрањен након 4 до 5 времена релаксације, или 90 секунди за пример изнад.
Производња наелектрисања се повећава са већим брзинама течности и већим пречницима цеви, постајући врло значајна у цевима пречника 200мм или већим. Британски стандард BS PD CLC/TR 50404:2003 (раније BS-5958-Part 2) Понашање при контроли нежељених статичких наелектрисања прописује максималне брзине протока. Због великог значаја на диелектричну константу, препоручена вредност за угљоводоничне течности које садрже воду је ограничен на 1 m/s.
Уземљавање је уобичајен начин за спречавање сакупљања наелектрисања. За течности које имају електричну проводљивост испод 10 pS/m уземљавање није довољно за дисипацију наелектрисања, већ је потребно додати анти-статичке адитиве.
Стандарди[уреди | уреди извор]
1.BS PD CLC/TR 50404:2003 Code of Practice for Control of Undesirable Static Electricity
2.NFPA 77 (2007) Recommended Practice on Static Electricity
3.API RP 2003 (1998) Protection Against Ignitions Arising Out of Static, Lightning, and Stray Currents
Електростатичка индукција у комерцијалној примени[уреди | уреди извор]
Принцип електростатичке индукције је коришћен много година у индустрији, почев од електростатичких индустријских система за фарбање аутомобила, бицикала и других производа.
Види још[уреди | уреди извор]
Референце[уреди | уреди извор]
- ^ Sadiku 2009, стр. 104.
Литература[уреди | уреди извор]
- Sadiku, Matthew (2009). Elements of electromagnetics. стр. 104. ISBN 9780195387759.
- Faraday, Michael (1839). Experimental Researches in Electricity. London: Royal Inst.
- e-book на пројекту Гутенберг
- Halliday, David; Resnick, Robert; Krane, Kenneth S. (1992). Physics. New York: John Wiley & Sons. ISBN 978-0-471-80457-4.
- Griffiths, David J. (1999). Introduction to Electrodynamics. Upper Saddle River, NJ: Prentice Hall. ISBN 978-0-13-805326-0.
- Haus, Hermann A.; Melcher, James R. (1989). Electromagnetic Fields and Energy. Englewood Cliffs, NJ: Prentice-Hall. ISBN 978-0-13-249020-7.
- William J. Beaty, "Humans and sparks; The Cause, Stopping the Pain, and 'Electric People". 1997.
- William Cecil Dampier, "The theory of experimental electricity". Cambridge [Eng.] University press, 1905 (Cambridge physical series). xi, 334 p. illus., diagrs. 23 cm. LCCN 05040419 //r33
- William Thomson Kelvin, Reprint of Papers on Electrostatics and Magnetism By William Thomson Kelvin, Macmillan 1872
- Alexander MacAulay Utility of Quaternions in Physics. Electrostatics—General Problem. Macmillan 1893
- Alexander Russell, A Treatise on the Theory of Alternating Currents. Electrostatics. University Press 1904
Спољашње везе[уреди | уреди извор]
- Man's static jacket sparks alert". BBC News, 16 September 2005.
- "Can shocks from static electricity damage your health?". Wolfson Electrostatics News pages.
- Invisible wall of static
- Downloadable electrostatic BEM modules in MATLAB for simple capacitance problems
- Introduction to Electrostatics: Point charges can be treated as a distribution using the Dirac delta function


















































