Конвергентни редови

У математици, ред је сума чланова низа бројева.

Дат је израз $\left\{a_{1},\ a_{2},\ a_{3},\dots \right\}$, н-та парцијална сума $S_{n}$ је збир првих н израза низа, који је,

$S_{n}=\sum _{k=1}^{n}a_{k}.$

Низ је конвергентан ако је низ његових парцијалних сума$\left\{S_{1},\ S_{2},\ S_{3},\dots \right\}$ конвергентан; Другим речима, он приближава одређени број. У формалном језику, низ конвергира ако постоји лимит $\ell$ такав да за било који произвољно мали позитиван број $\varepsilon >0$, постоји велики цео број $N$ такав да је свако $n\geq \ N$,

$\left|S_{n}-\ell \right\vert \leq \ \varepsilon .$

За сваку серија која се не конвергира се каже да је дивергентна.

Примери конвергентних и дивергентних редова

• Реципрочни бројеви позитивних целих бројева производе дивергентне редове (хармонијски редови):

  ${1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \over 5}+{1 \over 6}+\cdots \rightarrow \infty .$

• Наизменични знаци реципрочних позитивних целих бројева производе конвергентне редове:

  ${1 \over 1}-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}\cdots =\ln(2)$

• Реципрочни бројеви простих бројева производе дивергентне редове (тако да је скуп простих бројева "велики"):

  ${1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots \rightarrow \infty .$

• Реципрочни бројеви троугаоних бројева производе конвергентне редове:

  ${1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots =2.$

• Реципрочни бројеви факторијала производе конвергентне редове (види е):

  ${\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+\cdots =e.$

• Реципрочни бројеви квадратних бројева производе конвергентне редове (Базелски проблем):

  ${1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \over 25}+{1 \over 36}+\cdots ={\pi ^{2} \over 6}.$

• Реципрочни бројеви снаге 2 производе конвергентне редове (тако да је скуп снаге 2 "мали"):

  ${1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots =2.$

• Наизменични знаци реципрочних снага 2 такође производе конвергентне редове:

  ${1 \over 1}-{1 \over 2}+{1 \over 4}-{1 \over 8}+{1 \over 16}-{1 \over 32}+\cdots ={2 \over 3}.$

• Реципрочних бројеви Фибоначијевих бројева производе конвергентне редове (види ψ):

  ${\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{8}}+\cdots =\psi .$

Тестирање конвергенције

Постоји велики број метода којима се одређује ли је ред конвергентан или дивергентан.

Ако се за плаве редове, $\Sigma b_{n}$, може доказати да конвергирају, онда мањи редови, $\Sigma a_{n}$ морају да конвергирају. Контрапозиција, ако је за црвене редове, $\Sigma a_{n}$ доказано да дивергирају, онда $\Sigma b_{n}$ морају такође да дивергирају.

Тест поређења. Изрази низа $\left\{a_{n}\right\}$ су упоређени са онима другог низа $\left\{b_{n}\right\}$. Ако,

ѕа све n, $0\leq \ a_{n}\leq \ b_{n}$, и $\sum _{n=1}^{\infty }b_{n}$ конвергира, онда конвергира и $\sum _{n=1}^{\infty }a_{n}.$

Међутим, ако

ѕа све n, $0\leq \ b_{n}\leq \ a_{n}$, и $\sum _{n=1}^{\infty }b_{n}$ дивергира, онда дивергира и $\sum _{n=1}^{\infty }a_{n}.$

Тест односа. Претпотавимо да је за свако n, $a_{n}>0$. Претпоставимо да постоји $r$ такво да је

$\lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=r.$

Ако је r < 1, онда низ конвергира. Ако је r > 1, онда низ дивергира. Ако је r = 1, тест односа је неуверљив и низови могу да конвергирају или дивергирају.

Тест корена or Или тест н-тог корена. Претпоставимо да су у низу у изрази не-негативни. Дефинисати r као што следи:

$r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},$

где је "лим суп" означава границу супериор (евентуално ∞; уколико лимит постоји, он је иста вредност).

Ако је r < 1, онда низ конвергира. Ако је r > 1, онда низ дивергира. Ако је r = 1, тест корена је неуверљив и низови могу да конвергирају или дивергирају.

Тест односа и тест корена се заснивају на поређењу са геометријским низовима, и као такви се користе у сличним ситуацијама. У ствари, ако тест односа ради (што значи да ограничење постоји и није једнако 1), онда ради и тест корена; Обрнуто, међутим, није тачно. Тест корена је стога уопште могуе, али у практичном смислу границу је често тешко израчунати за најчешће виђене типове низова.

Тест интеграла. Низ се може упоредити са интегралом да се успостави конвергирање или дивергирање. Нека $f(n)=a_{n}$ буде позитиван и монотоно смањује функцију. Ако је

$\int _{1}^{\infty }f(x)\,dx=\lim _{t\to \infty }\int _{1}^{t}f(x)\,dx<\infty ,$

онда ред конвергира. Али, ако интеграл дивергира, онда то ради и низ.

Тест ограничења. Ако је $\left\{a_{n}\right\},\left\{b_{n}\right\}>0$, и граница $\lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}$ постоји и није нула, онда $\sum _{n=1}^{\infty }a_{n}$ конвергира ако и само ако $\sum _{n=1}^{\infty }b_{n}$ конвергира.

Тест наизменичних редова. Познат и као Лајбниц критеријум, тест наизменичних редова наводи да је за наизменични ред облика $\sum _{n=1}^{\infty }a_{n}(-1)^{n}$, ако је $\left\{a_{n}\right\}$монотоно опадајуће, а има ограничење од 0 у бесконачности, онда ред конвергира.

Тест коши кондензације. Ако је $\left\{a_{n}\right\}$ позитиван монотоно опадајући низ, онда  $\sum _{n=1}^{\infty }a_{n}$ конвергира ако и само ако $\sum _{k=1}^{\infty }2^{k}a_{2^{k}}$ конвергира.

Дириклетов тест

Абелов тест

Рабеов тест

 Условна и апсолутна конвергенција

Илустрација условне конвергенције снаге реда log(z+1) око 0 процењена на z = exp((π−​¹⁄₃)i). Дужина линије је бесконачна.

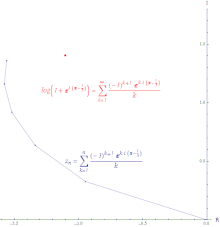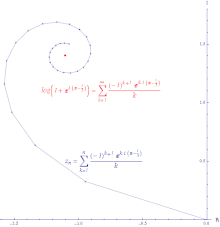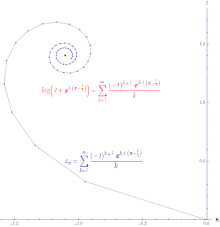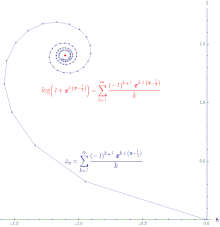
За било који ред $\left\{a_{1},\ a_{2},\ a_{3},\dots \right\}$, $a_{n}\leq \ \left|a_{n}\right\vert$ за било које н. Дакле,

$\sum _{n=1}^{\infty }a_{n}\leq \ \sum _{n=1}^{\infty }\left|a_{n}\right\vert .$

То значи да ако $\sum _{n=1}^{\infty }\left|a_{n}\right\vert$ конвергира, онда $\sum _{n=1}^{\infty }a_{n}$ такође конвергира (али не и обрнуто).

Ако ред $\sum _{n=1}^{\infty }\left|a_{n}\right\vert$ конвергира, онда је ред $\sum _{n=1}^{\infty }a_{n}$ апсолутно конвергентан. Апсолутно конвергентан ред је онај у ком се дужина линије створена спајањем свих корака у парцијалну суму и он је коначно дуг. Снага реда експоненцијалне функције апсолутно конвергира свуда.

Ако ред $\sum _{n=1}^{\infty }a_{n}$ конвергира, а ред $\sum _{n=1}^{\infty }\left|a_{n}\right\vert$ дивергира, онда је ред $\sum _{n=1}^{\infty }a_{n}$ условно конвергентан. Пут формиран повезивањем парцијалне суме условно конвергентног реда је бесконачно дуг. Снага реда логаритма условно конвергира.

Теорема Римановог реда тврди да је, ако низ условно конвергира, могуће преуредити услове низа на такав начин да низ конвергира за било коју вредност, или чак дивергира.

Јединствена конвергенција

Нека је $\left\{f_{1},\ f_{2},\ f_{3},\dots \right\}$ низ функције.   Низ равномерно конвергира за f ако је низ $\{s_{n}\}$ парцијалног збира дефинисан као

$s_{n}(x)=\sum _{k=1}^{n}f_{k}(x)$

конвергира јединствено за f.

Постоји аналог упоредног теста за бесконачни низ функције који се зове Веиерстрес М-тест.

Критеријум Кошијеве конвергенције

Критеријум Кошијеве конвергенције наводи да низ

$\sum _{n=1}^{\infty }a_{n}$

конвергира ако и само ако је низ парцијалног збира Кошијев низ. Ово значи да за свако $\varepsilon >0,$ постоји позитиван цео број $N$ такав да за свако $n\geq m\geq N$ постоји

$\left|\sum _{k=m}^{n}a_{k}\right|<\varepsilon ,$

што је еквивалентно

$\lim _{n\to \infty \atop m\to \infty }\sum _{k=n}^{n+m}a_{k}=0.$

Види још

• Гранична вредност низа
• Нормална конвергенција
• Листа математичких редова
• Дивергентни редови

Литература

• Bromwich, T. J. An Introduction to the Theory of Infinite Series MacMillan & Co. 1908, revised 1926, reprinted 1939, 1942, 1949, 1955, 1959, 1965.
• Dvoretzky, Aryeh; Rogers, C. Ambrose (1950). „Absolute and unconditional convergence in normed linear spaces”. Proc. Natl. Acad. Sci. U.S.A. 36 (3): 192—197. doi:10.1073/pnas.36.3.192.  MR0033975

Спољашње везе

• Hazewinkel, Michiel, ed. (2001), "Finite-difference calculus" Encyclopedia of Mathematics, Springer. ISBN 978-1-55608-010-4.
• Weisstein, Eric (2005). Riemann Series Theorem. Retrieved May 16, 2005.