Година








Година је време потребно да Земља обиђе око Сунца. Она је најдужа природна јединица за ток времена. Према референтној тачки у односу на коју се одређује пуни обилазак Земље око Сунца дефинисано је неколико година донекле различите дужине трајања:
- звездана или сидеричка година (365 d 6 h 9 min 9,76 s = 365,256363 d) је време обиласка Земље око Сунца с обзиром на систем далеких звезда;[1]
- тропска или Сунчева година (365 d 5 h 48 min 46 s = 365,24219 d) је време између два узастопна проласка Сунца кроз пролетну тачку;[2]
- аномалистичка година (365 d 6 h 13 min 52,6 s = 365,259636 d) је време потребно да Земља поновно прође кроз исту тачку на својој путањи, то јест кроз перихел;[3]
- еклипсна или драконистичка година (346 d 14 h 52 min 54 s = 346,620075 d) је време између два узастопна пролазака Сунца истим узлазним чвором Месечеве путање.
Звездана година важна је у механици кретања планета, док је тропска година раздобље у којем се годишња доба измене и зато је важна за свакодневни живот; њихова разлика узрокована је прецесијом Земље. Промена дужине аномалистичке године узрокована је закретањем линије апсида.[4]
Календарска година (Грегоријанског календара) траје 365 (обична година) или 366 дана (преступна година).
Време обиласка или револуције било које планете око Сунца назива се годином планете, па је на пример Марсова година, година на планети Марсу.[5][6]
Календарска година
[уреди | уреди извор]Календарска година означава раздобље између два истоимена датума (надневак) у календару. Календари се међусобно разликују према томе да ли је реч о соларним или лунарним календарима, или о њиховој комбинацији. Данас је најраширенији Грегоријански календар у којем једна календарска година траје 365 дана, а преступна година 366 дана. Његова се година дели на 12 месеци, а почиње 1. јануара и завршава 31. децембра. Календарска година има 52 или 53 недеље. Просечно календарска година грегоријанског календара траје 365,2425 дана или 365 дана, 5 сати, 49 минута и 12 секунди.
Просечно трајање календарске године Јулијанског календара, који је претходио грегоријанском, а и даље је у употреби у неким источним црквама, износи 365,25 дана или 365 дана и 6 сати.[7]
Звездана и тропска година
[уреди | уреди извор]Звездана година важна је у механици кретања планета, док је тропска година раздобље у којем се годишња доба измене и зато је важна за свакодневни живот; њихова разлика узрокована је прецесијом Земље.
Звездана година
[уреди | уреди извор]Звездана година или сидеричка година (365 d 6 h 9 min 9,76 s = 365,256363 d) је време обиласка Земље око Сунца с обзиром на систем далеких звезда. Звездана година важна је у механици кретања планета, док је тропска (Сунчева) година раздобље у којем се годишња доба измене и зато је важна за свакодневни живот; њихова разлика узрокована је прецесијом Земље, вртње која се одвија обратно од ротације Земље с периодом од 25 800 година (Платонова година). Годишњи износ Земљине прецесије јесте 50,29". Због периодичне промене положаја чворова Месечеве путање око Земље појављује се нутација, као набори на прецесијској купи, с периодом од 18,66 година (Саросов период). Земљина прецесија доводи до разлике између Сунчеве (тропске) и звездане (сидеричке) године. Звездана година је време потребно да Сунце на небеској сфери превали пун угао или, другим речима, време обилажења Земље око Сунца с обзиром на неки задани смер у простору (на пример у односу на пролетну точку). У Сунчевој (тропској) години Сунце превали небеском сфером угао који је од пуног угла мањи за износ Земљине прецесије; угао од 360° - 50,25" Сунце пређе за време Сунчеве године од 365,2422 дана, а угао од 360° за време звездане године. Звездана година је око 20 минута дужа од Сунчеве године.
Тропска година
[уреди | уреди извор]Тропска година, синодичка година или Сунчева година (365 d 5 h 48 min 46 s = 365,24219 d) је време између два узастопна пролазака Сунца пролетном тачком. Звездана година важна је у механици кретања планета, док је тропска година раздобље у којем се годишња доба измене и зато је важна за свакодневни живот; њихова разлика узрокована је прецесијом Земље. Земљина прецесија доводи до разлике између Сунчеве (тропске) и звездане (сидеричке) године. Звездана година је време потребно да Сунце на небеској сфери превали пун угао или, другим речима, време обилажења Земље око Сунца с обзиром на неки задани смер у простору (на пример у односу на пролетну тачку). У Сунчевој (тропској) години Сунце превали небеском сфером угао који је од пуног угла мањи за износ Земљине прецесије; угао од 360° - 50,25" Сунце пређе за време Сунчеве године од 365,2422 дана, а угао од 360° за време звездане године. Звездана година је око 20 минута дужа од Сунчеве године.[8]
Сунчево и звездано време
[уреди | уреди извор]У свакодневном деловању најважније раздобље времена одређено је изменом светлости и таме (дневном изменом осунчења или инсолације). Положај Сунца на небеској сфери преставља казаљку помоћу које се установљује доба дана. Рачунање времена дана почиње у поноћ, у часу када се Сунце налази у доњој кулминацији. Сунчев дан (синодички дан) је време које протече између Сунчеве две узастопне истоветне кулминације (горње у подне или доње у поноћ). Слично томе, звездани дан (сидерички дан) је време у којем пуни окрет учини нека звезда, или тачније речено пролетна тачка. Сунчево време служи за свакодневне животне делатности. Звезде су много мањег сјаја него Сунце. Звездано време потребно је да би се одредио положај звезда, а осим у астрономији, примењује се у геодезији и навигацији.[9]
Звездано време
[уреди | уреди извор]Казаљка звезданог времена је пролетна тачка. Звездано вријеме једнако је сатном углу пролетне тачке. Звездани дан почиње када се прољетна тачка налази у горњој кулминацији. Звездано време повезано је у сваком часу са сатним углом и ректасцензијом звезде. Оно је ограничено тиме на раздобље од 0 до 24 h. Звездано време тече онолико једнолико колико се једнолико Земља окреће. Ток звезданог времена одређен је само Земљином вртњом у односу на звезде. У току времена постоје мале промене. Разлози тих промена су тројаки. Један је учинак плиме. При кретању плимних таласа долази до трења између водених маса и дна. Трењем се губи део кинетичке енергије ротације па се она успорава. Појава се манифестује у вековним размацима. Затим, постоје сезонске промене брзине вртње јер се зависно од годишњег доба мењају јачине и смерови ветрова те морских струја. Стога се ротација и успорава и убрзава у току године, зависно од тога помажу ли струјања Земљиној ротацији или одмажу. Трећи разлог крије се у кретањима у Земљиној унутрашњости и у физичком простору Земљине околине.
Сунчев дан задан је не само Земљином ротацијом око властите осе, већ и Земљином годишњом путањом око Сунца. Притом Земља учини један окрет више око своје осе, с обзиром на пролетну тачку (или звезде) него с обзиром на Сунце. Обилажење око Сунца чини један додатни окрет Земље према систему звезда. То значи да ће број звезданих дана у Сунчевој (тропској) години бити за јединицу већи од броја Сунчевих дана у Сунчевој години:
- (T + 1) звездани дан = T Сунчев дан
где је T - Сунчева или тропска година која износи 365 d 5 h 48 min 46 s = 365,24219 d, па се добија:
- 1 звездани дан = 23 h 56 min 4 s
Звездани дан дели се сам по себи у 24 h звезданог времена, а сати, минуте и секунде звезданог времена такође трају краће од сата, минута и секунди Сунчевог времена:
- 1 звездани сат = 59 min 50 s
- 1 звездана минута = 59,8 s
Звездано време зависи од годишњег доба. Оног часа када је Сунце у пролетној тачки с којом заједно пролази кроз горњу кулминацију подне је (12 h Сунчевог времена), али истодобно је и почетак звезданог дана (0 h звезданог времена). Наредног ће се дана Сунце наћи источније од пролетне тачке, јер оно међу звездама одмиче на исток, па ће у дневној ротацији неба „заостајати“ за звездама и касније проћи него пролетна тачка. Када угао између сатног круга пролетне тачке и Сунца порасте на 90° (почетак лета), звездано ће време бити „млађе“ од Сунчевог за 6 h; када порасте на 180° (почетак јесени), звездано време једнако је Сунчевом; када разлика досегне 270° (почетак зиме), звездано ће време бити за 6 h „старије“ од Сунчевог.
Средњи Сунчев дан
[уреди | уреди извор]Сунце се не креће једноликом брзином по еклиптици, а еклиптика се не подудара с небеским екватором. По еклиптици се Сунце не креће једнолико, јер његово привидно кретање само одражава право кретање Земље око Сунца; Земља се по еклиптичној стази креће промењивом брзином. Стога Сунце не прелази сваког дана једнаке углове по еклиптици. Сунце исто мења своју угаону удаљеност од небеског екватора. То значи да оно осим кретања упоредо с небеским екватором изводи још и кретање у смеру нормалном на екватор. На пример, дан после почетка пролећа, Сунце ће се наћи нешто северније од небеског екватора. Дневни помаци на север или на југ од небеског екватора највећи су у доба равнодневница, а у доба око солстиција Сунце се креће упоредо с небеским екватором. То значи, и када би се Сунце еклиптиком и кретало равномерно, његова се пројекција на небески екватор не би кретала равномјерно.
Прави Сунчеви дани не трају зато једнако. Средњи Сунчев дан (или напросто дан) је просек свих правих Сунчевих дана у току тропске или Сунчеве године. Данас се трајање средњег Сунчевог дана прати помоћу атомских сатова. Године 1967. договорено је да се уместо секунде одређене из кретања Земље, као јединица времена користи атомска секунда или секунда одређена атомским сатом. Та је секунда повезана с трајањем тропске или Сунчеве године 1900. Секундом се сматра раздобље времена који је био 31 556 925,9747 пута садржан у тој тропској години. Како се дужина дана и тропске године с временом мењају, то се ради усклађења времена дана с календаром убацује у календарски дан додатна (прекобројна) секунда.
Једначина времена
[уреди | уреди извор]Природне појаве, као што су излазак и залазак Сунца, те горња кулминација (право месно подне), зависе од кретању правог Сунца. Да би се тренутак дана повезао са сатном кружницом на којој се налази Сунце, установљена је разлика правог и средњег Сунчевог времена.[10][11][12] Разлика је позната под називом једначина времена:
- једначина времена = право Сунчево време - средње Сунчево време
Средње Сунчево време
[уреди | уреди извор]Пошто се свако време, и звездано и Сунчево, мери сатним углом (у односу на меридијан посматрача), оно је локалног карактера.[13] Свака географска дужина има своје време. Ако је на датом месту подне, западно од њега ће још бити јутро, а источније од ће бити поподне. Сваких 15° географске дужине доноси разлику месних времена од 1 сата. Зато је на некој географској дужини λ, средње Сунчево време једнако:
- Tm = UT ± λ
Код источних географских дужина предзнак је позитиван, код западних негативан. Светско или универзално време УТ (енг. Universal Time) средње је Сунчево време на 0° меридијану или гриничком меридијану. Земљописну дужину λ треба изразити у временским јединицама користећи следеће односе: 1 h = 15°; 1 min = 15'; 1 s = 15"; 1° = 4 min; 1' = 4 s; 1" = 0,066 s.
Координирано светско вријеме УТЦ
[уреди | уреди извор]У друштвеним заједницама успостављено је појасно или зонско време. Уместо да се свако место равна по својем средњем Сунчевом времену које започиње у месну поноћ, читаве државе или њихови делови имају заједничко време. Цела је Земља расподељена на 24 временске зоне или појаса. Средишњи меридијани временске зоне размакнути су за 15°. Унутар сваке зоне поштује се јединствено време. Поједине државе су увеле и летње рачунање времена (енг. Daylight saving time или ДСТ), којим се током љетних месеци, казаљке пребацују обично за један сат унапред у односу на координирано светско време (енг. Coordinated Universal Time или УТЦ). На Балкану се примењује средњоевропско време или УТЦ+1 (тачније речено средњоевропско зимско време), које је одређено средњим Сунчевим временом за источну географску дужину од 15° Е, а од 1983. примењује се и летње рачунање времена. Када се жели исказати временски след појава опажаних на различитим земљописним дужинама, као и праве временске разлике, тренутак времена изражава се помоћу координираног светског времена УТЦ.
Право Сунчево време
[уреди | уреди извор]Односи правог и средњег Сунчевог времена, месног и зонског, користе се када се жели сазнати колико је сати у тренутку правог времена. Грађанско време које се нормално примењује је средње Сунчево време само за одређени меридијан. На Балкану је то 15° Е меридијан. На локацији која је 1° источније, на 16° Е меридијану, средње време ће бити за 4 минуте „старије“ (средњем Сунчевом времену треба додати 4 минуте).
Датумска граница
[уреди | уреди извор]Тренутак поноћи у некој временској зони одељује прошли дан од идућег дана. Дакле, постоји једна природна граница датума (надневка) која се непрестано покреће од временске зоне до зоне. Зато на Земљи мора постојати још једна граница датума, јер два подручја на Земљи, која истодобно имају два различита датума, морају се сучељавати на две, а не само на једној граници. Зато је постављена чврста датумска граница, и то у најмање насељеном подручју Тихог океана. Са обе стране границе исто је време у дану, јер је једнака осунчаност, али се сусрећу два различита датума. Изводи се правило да приликом преласка датумске границе треба један дан одузети при путовању са запада на исток, а додати један дан при путовању се са истока на запад. Путовањем на исток путник залази у подручје све „старијег“ дана, мора помицати сатну казаљку непрестано унапријед, па на читавом кругу око Земље напуни један дан. Зато се стекне један дан више, па се при преласку датумске границе он мора одбити.
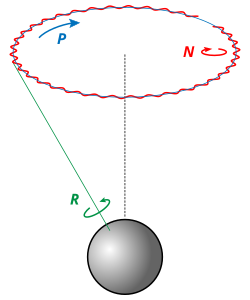
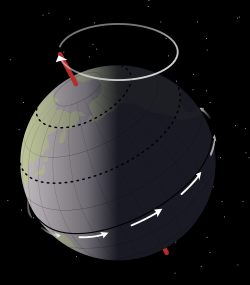
Земљина прецесија и нутација
[уреди | уреди извор]Осим ротације и обилажења око Сунца (револуције), Земља показује још једну врсту кретања. Њена оса такође се непрестано креће и описује купу око пола еклиптике, и то у смислу левог вијка који напредује на север. Вршни полуугао купе једнак је нагибу еклиптике (еклиптика је нагнута је под углом од 23°27′ према небеском екватору). Због тога закретања осе у истом се смислу закреће и пресециште равни еклиптике с небеским екватором, а с њиме и пролетна тачка. Зато пролетна тачка мења место међу звездама. Помак пролетне тачке одвија се у смеру дневне вртње неба, а то је управо супротно од привидног, годишњег кретања Сунца: пролетна тачка се креће на запад, а Сунце на исток. То значи да пролетна тачка иде у сусрет Сунцу, или „пред“ Сунце. Отуда потиче латински назив те појаве, јер praecedere значи ићи напред.
Земљину прецесију тумачи механика ротирајућег угаоног тела. Најјачи утицај на њу показују Месец и Сунце. Месец је делотворнији зато што је много ближи. Заједнички учинак Месеца и Сунца назива се луни-соларном прецесијом. Међутим док се Сунце налази увек у равнини еклиптике, Месечева стаза је према њој нагнута отприлике за 5°. Отуда долази до периодичке промене Месечевог утицаја, у времену од 18.66 година (то је период регресије чворова Месечеве стазе), па прецесијска купа није сасвим глатка него испуњен наборима. Појава набора назива се нутација.
Општа прецесија
[уреди | уреди извор]Величина луни-соларне прецесије износи 50,37" на годину. То је угао за који би се по еклиптици помакнула пролетна тачка када би деловали само Мјесец и Сунце. Међутим утичу још и планете. Њихов се учинак или планетска прецесија истиче као промена положаја равни еклиптике. Под привлачном силом планета, Земља се њише око 0,05" на годину (у данашње време). Због тога ће пролетна тачка клизити и по небеском екватору за 0,13" на годину, па ће у смеру еклиптичких дужина укупан помак износити 50.25" на годину. То је годишњи износ опште Земљине прецесије.
Земљина прецесија доводи до разлике између Сунчеве (тропске) и звездане (сидеричке) године. Звездана година је време потребно да Сунце на небеској сфери превали пуни угао или, другим речима, време обилажења Земље око Сунца с обзиром на неки задани смер у простору (нпр. у односу на пролетну тачку). У Сунчевој години Сунце превали небеском сфером угао који је од пуног угла мањи за износ Земљине прецесије; угао од 360° - 50,25” Сунце пређе за време Сунчеве године од 365,2422 дана, а угао од 360° за време звездане године. Звездана година је око 20 минута дужа од Сунчеве године.
Платонова година
[уреди | уреди извор]Из износа опште прецесије лако се налази раздобље времена у којем Земљина оса обиђе прецесијску купу, а пролетна тачка пуни круг по небеском екватору. Ако помак у једној години износи 50,25", тада за помак од 360° треба 25 800 година. То је Платонова година. У том раздобљу небески пол опише кружницу међу звездама. Стога ће данашњу Северњачу (α Малог медведа) замењивати друге звезде. Пре 5000 година забележена је као Северњача звезда Тубан (α Змаја). Око године 14 000. као Северњача ће служити звезда Вега, иако северном небеском полу неће прићи ближе од 5°. Од времена када су астрономи именовали сазвежђа и установили Земљину прецесију, пролетна се тачка помакнула из сазвежђа Овна у сазвежђе Риба, а тако су се у суседно сазвежђе помакнуле и остале главне тачке еклиптике. Знакови тих тачака остали су међутим исти као што су и били. С помаком пролетне тачке повезана је највише и промена звезданих ректасцензија, док је промена деклинација много мања.
Дужине разних типова година
[уреди | уреди извор]- 353, 354 или 355 дана — дужине регуларних година у неким лунисоларним календарима
- 354,37 дана — 12 лунарних месеци; просечна дужина године у лунарним календарима
- 365 дана — обична година у многим соларним календарима; ~31,53 милиона секунди
- 365,24219 дана — просечна тропска година близу 2000. године
- 365,2424 дана — година пролећне равнодневнице
- 365,2425 дана — просечна дужина године у Грегоријанском календару
- 365,25 дана — просечна дужина године у Јулијанском календару; светлосна година се базира на овој години; износи 31.557.600 секунде
- 365,2564 дана — звездана година или сидеричка година
- 366 дана — преступна година у многим соларним календарима; 31,62 милиона секунди
- 383, 384 или 385 дана — дужине преступних година у неким лунисоларним календарима
- 383,9 дана — 13 лунарних месеци; преступна годинама у неким лунисоларним календарима
Просечна Грегоријанска година износи 365,2425 дана = 52,1775 седмица = 8.765,82 часова = 525.949,2 минута = 31.556.952 секунди (просечна соларна, не СИ).
Просечна Јулијанска година износи 365,25 дана.[14]
Обична или проста година износи 365 дана = 12 месеци = 8.760 часова = 525.600 минута = 31.536.000 секунди.
Преступна година износи 366 дана = 12 месеци = 8.784 часова = 527.040 минута = 31.622.400 секунди.
400-годишњи циклус Грегоријанског календара има 146097 дана и стога тачно 20871 недељу.
400-годишњи циклус Јулијанског календара има 146100 дана, односно 20871 недељу и 3 дана.
Симболи
[уреди | уреди извор]- ka (kiloannum) – јединица времена једнака хиљаду или 103 година (1 E3), у антропологији познат под именом миленијум. Користи се у геологији, палеонтологији и археологији.
- Ma (megaannum) – јединица времена једнака милион или 106 година (1 E6). Користи се у геологији, палеонтологији и небеској механици.
- Ga (gigaannum) – јединица времена једнака 109 година или милијарду година. Користи се у космологији и геологији.[15]
- Ta (teraannum) – јединица времена једнака 1012 година или трилион година.
- Pa (petaannum) – јединица времена једнака 1015 година или квадрилион година.
- Ea (exaannum) – јединица времена једнака 1018 година или квинтилион година.
Види још
[уреди | уреди извор]Референце
[уреди | уреди извор]- ^ International Earth Rotation and Reference System Service. (2010).IERS EOP PC Useful constants.
- ^ Richards, E. G. . Calendars. In S. E. Urban & P. K. Seidelmann (Eds.), Explanatory Supplement to the Astronomical Almanac (3rd ed.). Mill Valley, CA: University Science Books.. (2013). стр. 586.
- ^ Astronomical Almanac for the Year 2011. Washington and Taunton: US Government Printing Office and the UK Hydrographic Office. 2009. стр. A1, C2.
- ^ Astronomical Almanac for the Year 2011. Washington and Taunton: U.S. Government Printing Office and the U.K. Hydrographic Office. 2009. стр. M18 (Glossary). Архивирано из оригинала 19. 08. 2017. г. Приступљено 25. 07. 2017.
- ^ OED, s.v. "year", entry 2.b.: "transf. Applied to a very long period or cycle (in chronology or mythology, or vaguely in poetic use)."
- ^ Година, „Хрватска енциклопедија“, Лексикографски завод Мирослав Крлежа, www.enciklopedija.hr, 2015.
- ^ International Astronomical Union "SI units" accessed February 18, 2010. (See Table 5 and section 5.15.) Reprinted from George A. Wilkins & IAU Commission 5, "The IAU Style Manual (1989)" (PDF file) in IAU Transactions Vol. XXB
- ^ Ziggelaar, A. (1983). "The Papal Bull of 1582 Promulgating a Reform of the Calendar". In Coyne, Hoskin, Pedersen (eds), Gregorian Reform of the Calendar: Proceedings of the Vatican Conference to Commemorate its 400th Anniversary. Vatican City: Pontifical Academy of Sciences, Specolo Vaticano. стр. 223
- ^ Владис Вујновић : "Астрономија", Школска књига, 1989.
- ^ U.S. Naval Observatory Nautical Almanac Office and Her Majesty's Nautical Almanac Office (2010). Astronomical Almanac for the year 2011. Washington: U.S. Government Printing Office. стр. C2, L8.
- ^ Simon, J.L.; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. (1994). „Numerical expressions for precession formulae and mean elements for the Moon and planets”. Astronomy and Astrophysics. 282 (2): 663—683. Bibcode:1994A&A...282..663S.
- ^ Taff, Lawrence G. (1985). Celestial Mechanics: A Computational Guide for the Practitioner. New York: John Wiley & Sons. стр. 103. ISBN 978-0-471-89316-5.
- ^ Seidelmann, P. Kenneth (2013). Explanatory Supplement to the Astronomical Almanac. Sean E. Urban (ed.) (3 изд.). Univ Science Books. стр. 587. ISBN 978-1-891389-85-6.
- ^ Shields, Miriam Nancy. (1924). "The New Calendar of the Eastern Churches, Popular Astronomy, Vol. 32. стр. 407. Courtesy NASA Astrophysics Data System.
- ^ Arndt, Nicholas (2011), „Ga”, Ур.: Gargaud, Muriel; Amils, Ricardo; Quintanilla, José Cernicharo; Cleaves, Henderson James (Jim), Encyclopedia of Astrobiology (на језику: енглески), Berlin, Heidelberg: Springer, стр. 621, ISBN 978-3-642-11274-4, doi:10.1007/978-3-642-11274-4_611, Приступљено 22. 12. 2020
Литература
[уреди | уреди извор]- Taff, Lawrence G. (1985). Celestial Mechanics: A Computational Guide for the Practitioner. New York: John Wiley & Sons. стр. 103. ISBN 978-0-471-89316-5.
- Astronomical Almanac for the Year 2011. Washington and Taunton: US Government Printing Office and the UK Hydrographic Office. 2009. стр. A1, C2.
- U.S. Naval Observatory Nautical Almanac Office and Her Majesty's Nautical Almanac Office (2010). Astronomical Almanac for the year 2011. Washington: U.S. Government Printing Office. стр. C2, L8.
- Astronomical Almanac for the Year 2011. Washington and Taunton: U.S. Government Printing Office and the U.K. Hydrographic Office. 2009. стр. M18 (Glossary). Архивирано из оригинала 19. 08. 2017. г. Приступљено 25. 07. 2017.
- Astronomical Almanac for the Year 2011. Washington and Taunton: US Government Printing Office and the UK Hydrographic Office. 2009. стр. A1, C2.
- Fraser, Julius Thomas (1987). Time, the Familiar Stranger (illustrated изд.). Amherst: University of Massachusetts Press. ISBN 978-0-87023-576-4. OCLC 15790499.
- Whitrow, Gerald James (2003). What is Time?. Oxford: Oxford University Press. ISBN 978-0-19-860781-6. OCLC 265440481.
